Glossar
Polyeder
Polyeder sind geometrische Körper, die aus Ecken, Kanten und ebenen vieleckigen Seitenflächen bestehen. In unserem Projekt beschränken wir uns auf konvexe Polyeder. Das bedeutet, dass alle inneren Winkel kleiner sind als 180°, also dass sie keine Einbuchtungen, Aushöhlungen oder Löcher haben.
Bekannte Beispiele von Polyedern sind der Würfel oder die Pyramide. Aber auch das Prisma oder das Oktaeder sind manchem vielleicht schon einmal begegnet. Es gibt aber noch viel mehr Polyeder.
Eine besonders symmetrische und regelmäßige Klasse von Polyedern sind die platonischen Körper. Die fünf Polyeder bestehen nur aus gleichseitigen Vielecken. Das Tetraeder, das Oktaeder und das Ikosaeder bestehen aus gleichseitigen Dreiecken. In jeder Ecke des Tetraeders treffen drei davon zusammen. Beim Oktaeder sind es vier und beim Ikosaeder fünf. Legt man nun aber sechs gleichseitige Dreiecke in einem Punkt zusammen, so ergibt sich ein Gesamtwinkel von 360°. Damit liegen die Dreiecke flach auf der Ebene und kein Körper entsteht. Ähnlich konstruiert man auch den Würfel, bei dem in jeder Ecke drei Quadrate zusammenstoßen und das Dodekaeder, in dem je drei Fünfecke aneinander treffen. Dieses Vorgehen verwendete auch Euklid, der in seinem Buch „Elemente“ auf diese Weise bewies, dass es keine weiteren Körper mit dieser Eigenschaft geben kann.


Doch nicht nur symmetrische Polyeder sind für Mathematikerinnen und Mathematiker interessant. Oft suchen sie Polyeder (oder eben ihr höherdimensionales Äquivalent, Polytope), die ganz bestimmte Eigenschaften haben. Wir haben Geometerinnen und Geometer (so heißen die Mathematikerinnen und Mathematiker, die sich mit Geometrie beschäftigen) gefragt, welches ihre Lieblingspolyeder sind und warum. Hier sind einige Antworten:
„Wenn man Polyeder als Edelsteine betrachtet, so ist das Assoziaeder (Artikel in Englisch) der Diamant unter den Polyedern. Diamanten bestehen aus einem in der Natur sehr häufig vorkommenden Element: Kohlenstoff. Genauso entsteht das Assoziaeder durch sehr verbreitete Verfahren. Es fasziniert aber dennoch durch seine einzigartige und besondere Struktur – wie eben der Diamant.“ - Jean-Philippe Labbé.
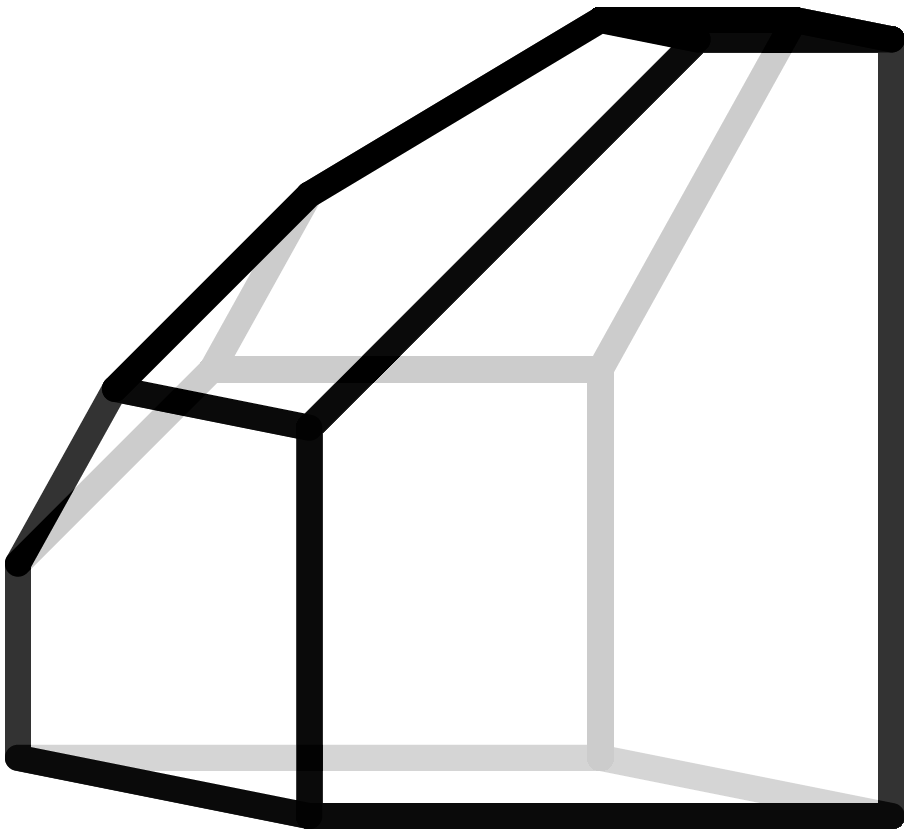
„Mein Lieblingspolyeder ist das Ikosaeder, denn es ist sowohl sehr komplex als auch sehr einfach. Wenn man anfängt gleichseitige Dreiecke aneinander zu kleben, immer fünf Stück an einer Ecke, entsteht zwangsläufig dieses schöne Stück. Wenn ich mich in der Schule gelangweilt habe – auch das ist vorgekommen – habe ich angefangen Ikosaeder an den Rand meiner Hefte zu zeichnen. Manchmal waren sie natürlich nicht so regelmäßig, ich habe mir einen Spaß daraus gemacht, sie wie Gesichter aussehen zu lassen. Ein weiterer Grund für meine Faszination ist, dass man seine 12 Ecken in 3 Vierecke zerlegen kann, die dem goldenen Schnitt entsprechen und wie borromäische Ringe ineinander verschlungen sind.“ - Francisco Santos.

„Das interessanteste Polyeder ist für mich der ‚Miller-Körper‘ (Artikel in Englisch), der auch als ‚Pseudorhombenkuboktaeder‘ oder als ‚verlängerte verdrehte Quadratsdoppelkuppel‘ bezeichnet wird. Zuerst entdeckt wurde er im Jahre 1905 von D.M.Y. Sommerville. Er hat eine bewegte Geschichte des Übersehen-, Entdeckt- und Wiederentdecktwerdens. (Unter anderem auch von J.C.P. Miller, dem es einen seiner Namen verdankt.) Bei näherer Betrachtung entdeckt man eine Verdrehung des scheinbar perfekten Körpers, der seine Schönheit unterstreicht. Zunächst erscheint er sehr klassisch, wie ein Archimedischer Körper. Nach der modernen Definition dieser Körper gehört er dieser Familie aber nicht an. Darum ist das Pseudorhombenkuboktaeder auch eine Erinnerung daran, dass wir in der Mathematik sorgfältig mit Definitionen umgehen müssen und es immer Ausnahmen und Spezialfälle geben kann, die man zunächst nicht bedacht hat.“ - Günter M. Ziegler.
„Die Klasse der Koebe-Polyeder faszinieren mich. Alle ihre Kanten berühren eine Kugel und alle Seitenflächen besitzen einen Innkreis. Die Innkreise von benachbarten Seitenflächen berühren sich in einem Punkt. Es existiert ein expliziter Dualisierungsprozess, mit dem diese diskreten Minimalflächen von Koebe Polyedern generiert werden können. Die dazugehörigen Flächen sind die diskreten P-Schwarz-Flächen und das Koebe-Polyeder ist seine Gauß-Abbildung. Mehr dazu kann man hier nachlesen: A.I. Bobenko, T. Hoffmann, B.A. Springborn, Minimal surfaces from circle patterns: Geometry from combinatorics, Ann. of Math. 164:1 (2006) 231-264) oder nachschauen: (http://discretization.de/en/movies/koebe/).“ - Alexander Bobenko.
Polygon
Ein Polygon, das man umgangssprachlich auch Vieleck nennt, ist ein zweidimensionales Polyeder. Es besteht aus Ecken und Kanten. Die Fläche, die von den Kanten eingegrenzt wird, ist das Polygon selbst.
Eine besondere Klasse bilden die regulären Polygone. Sie bestehen nur aus Kanten gleicher Länge, und alle ihre inneren Winkel sind gleich groß. Das Quadrat, das gleichseitige Dreieck und auch das gleichseitige Fünfeck sind reguläre Polygone. Sie bilden die Bausteine für die Platonischen und Archimedischer Körper.
Polyedernetz
Schneidet man einen hohlen Würfel an ausreichend vielen Kanten auf und faltet ihn dann flach auf die Ebene auf, so entsteht ein Würfelnetz. Zeichnet man dieses Netz auf Papier oder Pappe, so entsteht ein Bastelbogen, den man ausschneiden und zu einem Würfel zusammenkleben kann. Diese Methode funktioniert natürlich auch für alle anderen Polyeder. In unserem Projekt nutzen wir genau diese Bögen, um die Modelle zu bauen. Das Polyeder wird an den Kanten aufgeschnitten und ausgeklappt. Diesen Vorgang haben wir mit dem Computer simuliert und auf diese Weise automatisch die Polyedernetze erstellt.
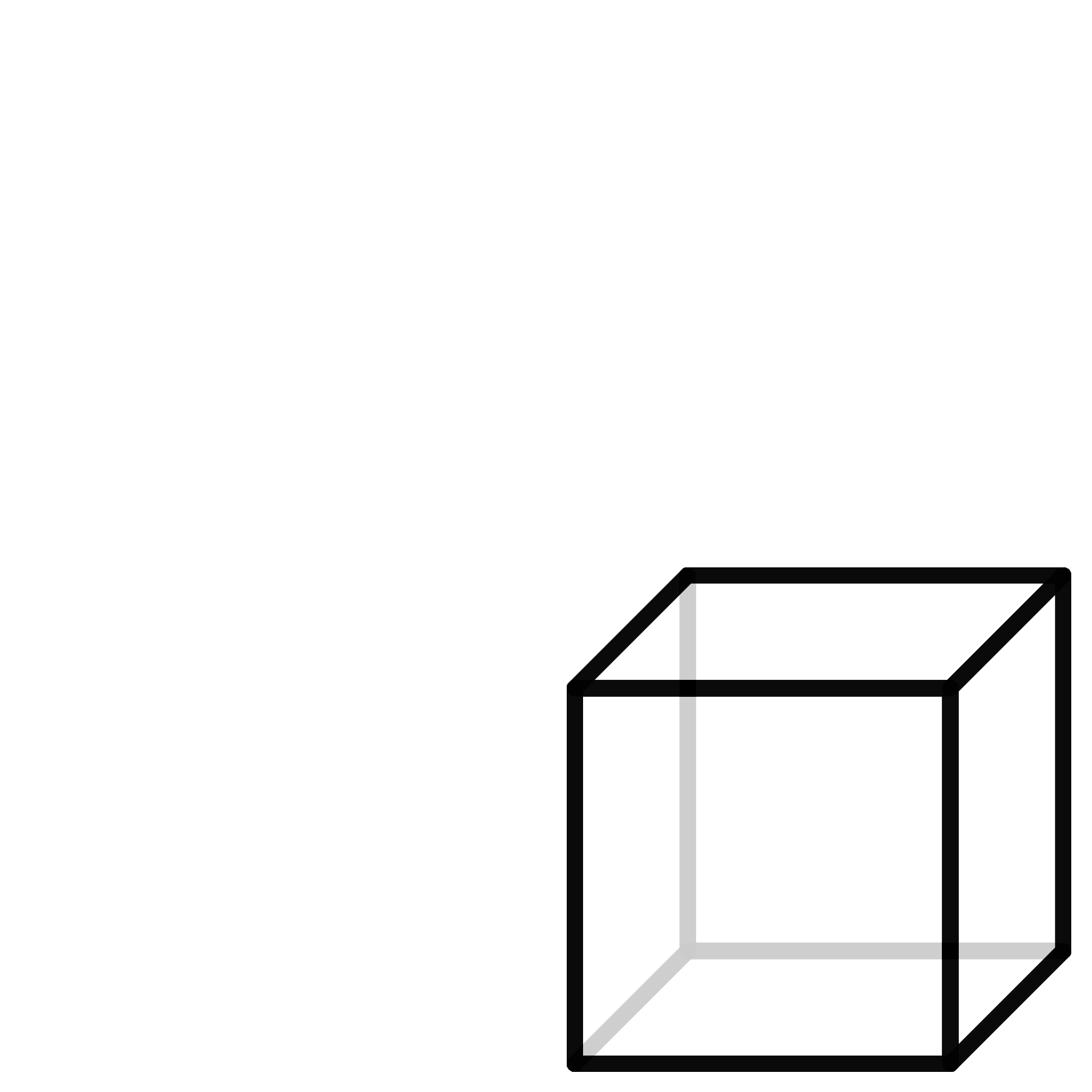
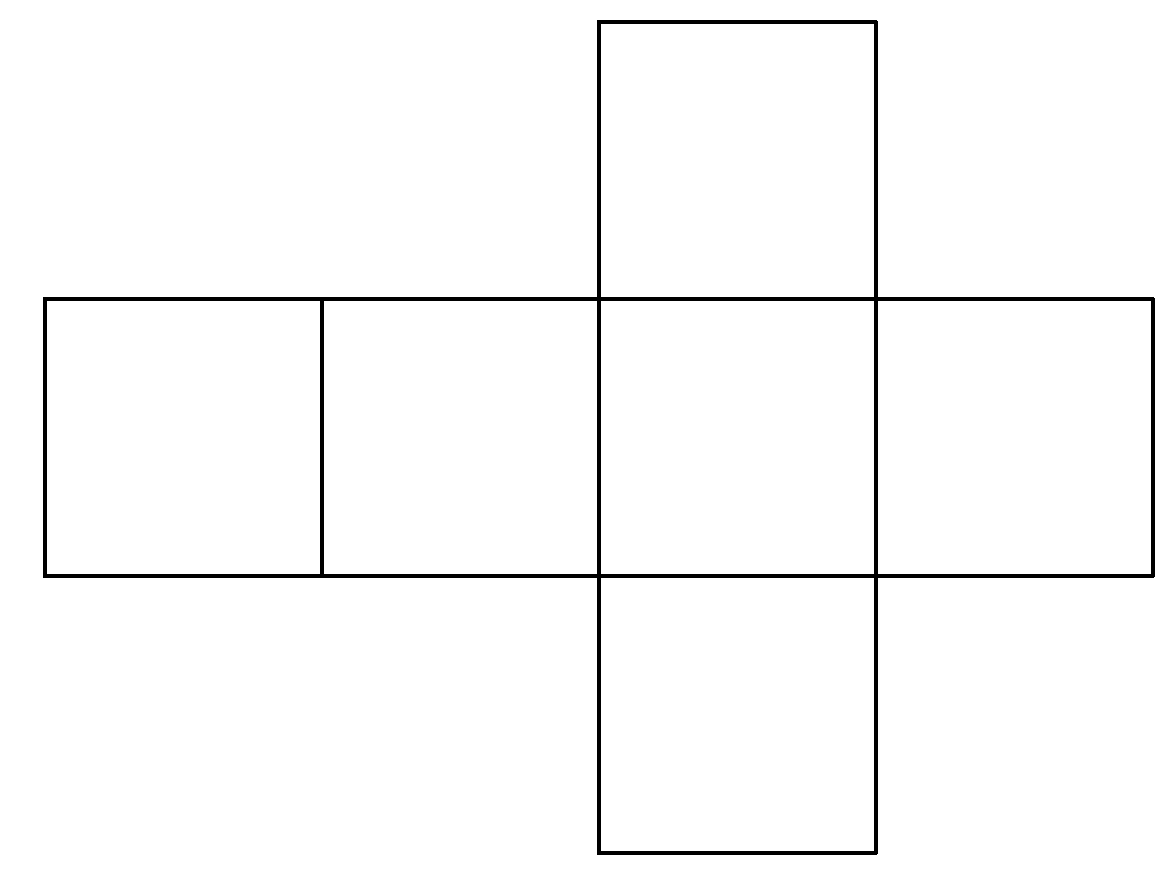
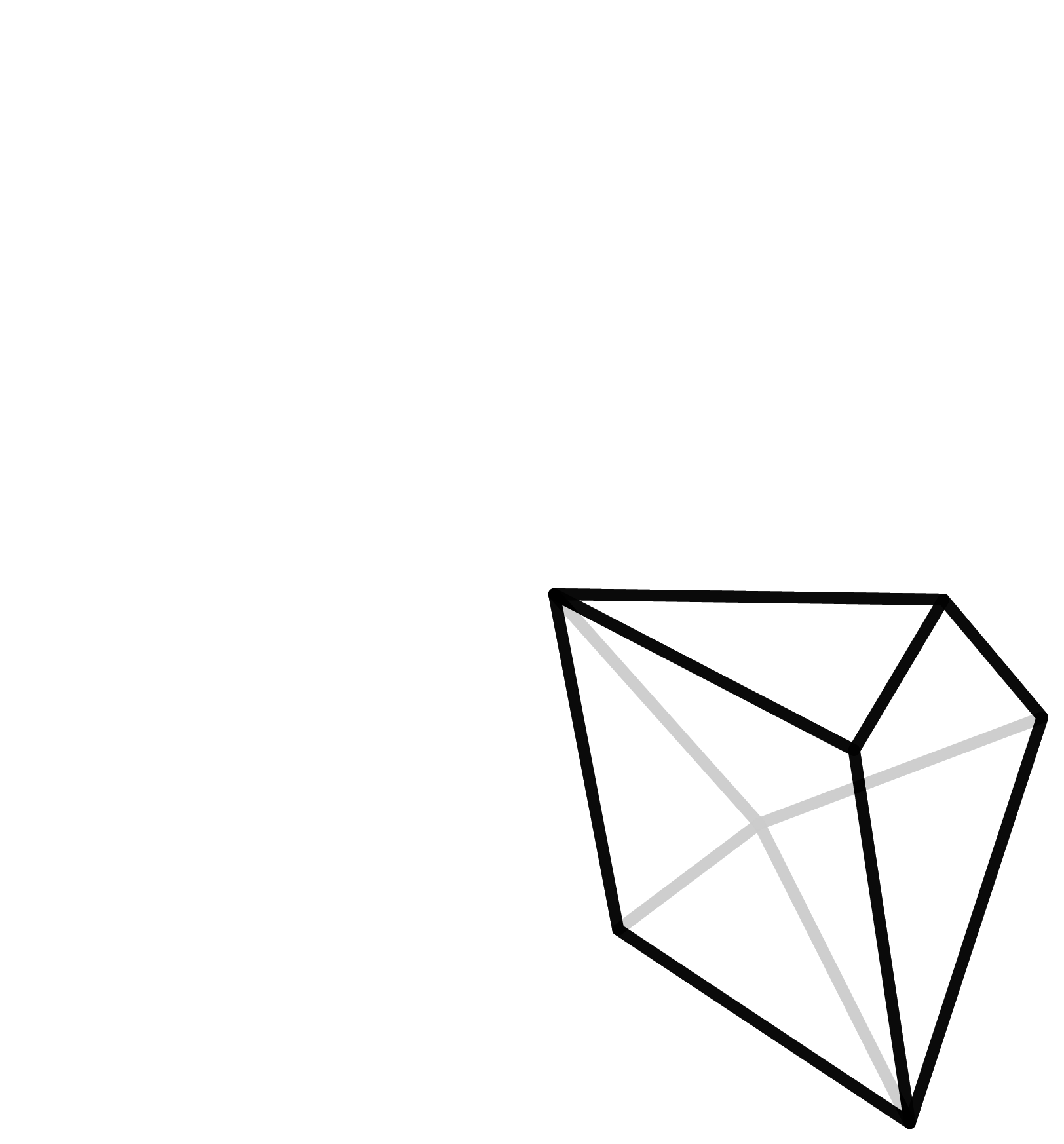
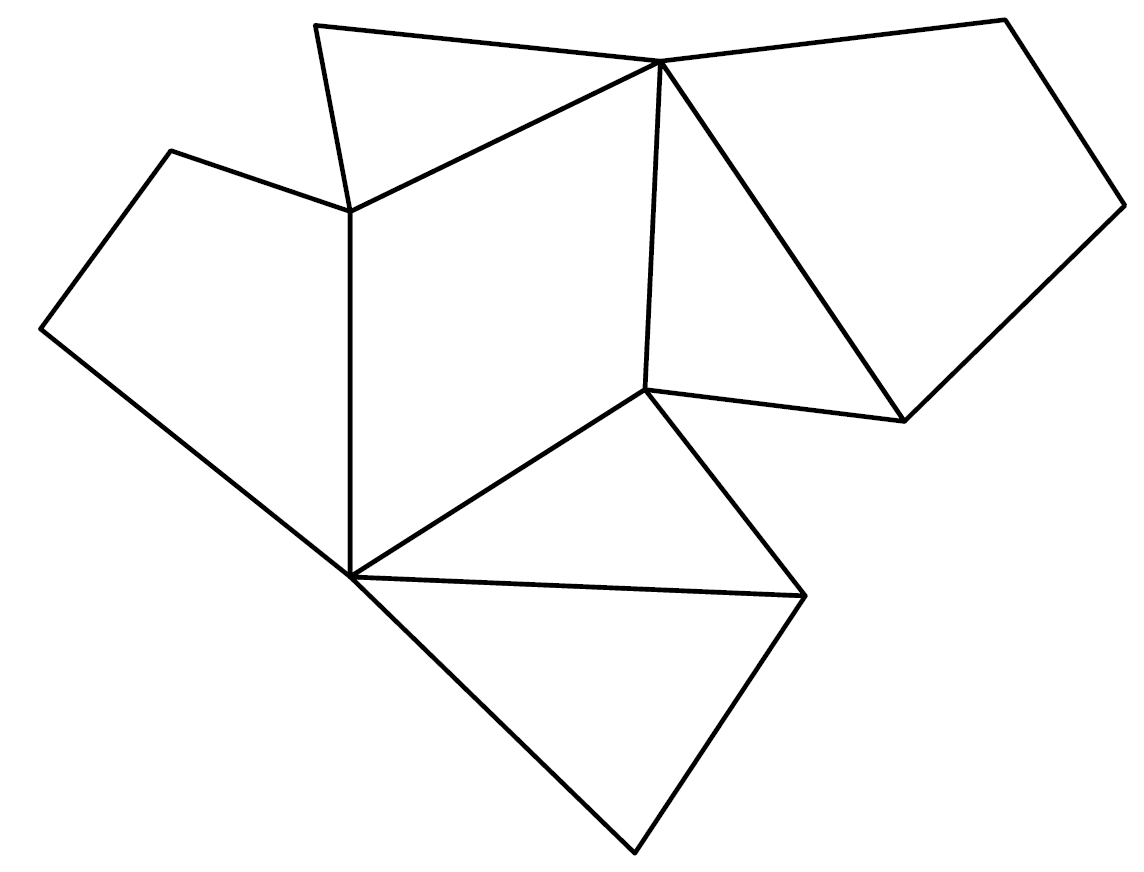
Ein Würfel mit seinem Netz sowie ein Polyeder mit sieben Ecken und das dazugehörige Netz.
Archimedische Körper
Die archimedischen Körper bilden eine weitere Klasse von sehr symmetrischen und damit manchmal als schön bezeichneten Polyedern. Auch sie bestehen nur aus gleichseitigen Vielecken, aber, anders als bei den platonischen Körpern, nicht nur aus denselben. Der Fußball ist wohl der bekannteste archimedische Körper. Mathematikerinnen und Mathematiker nennen ihn auch Ikosaederstumpf, denn er entsteht, wenn man bei einem Ikosaeder an jeder Ecke die Spitze abschneidet.

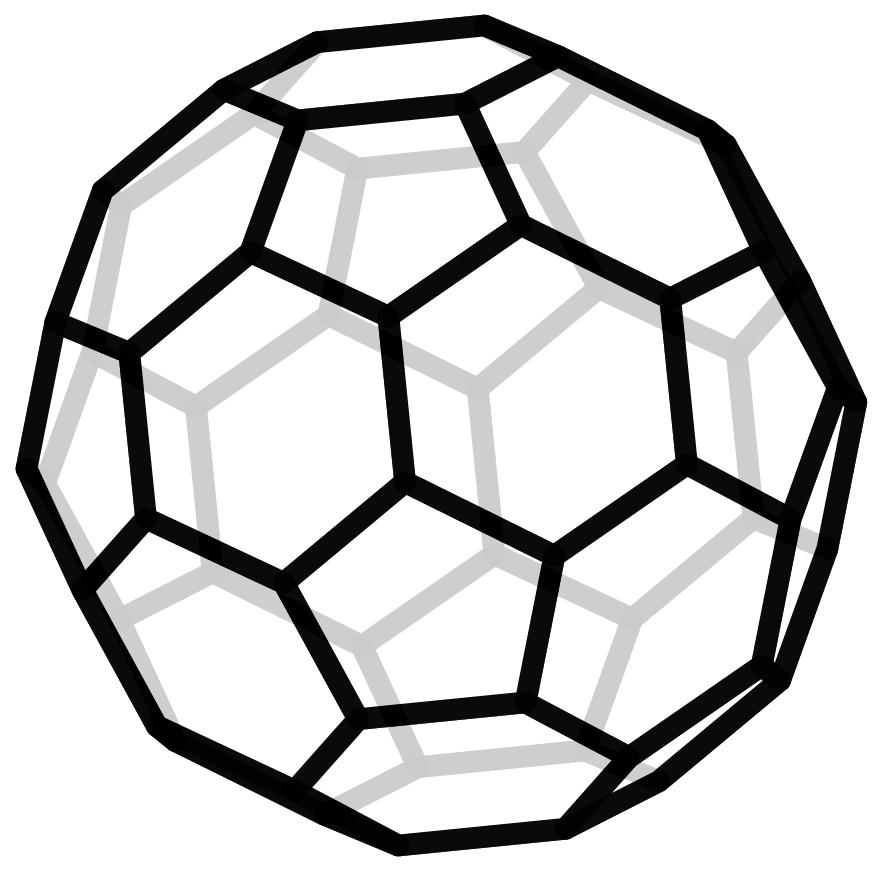
Links der Ikosaeder und rechts sein Ikosaederstumpf (oder Fußball).
Wie viele Polyeder gibt es?
Für jede feste Anzahl an Ecken gibt es eine bestimmte Anzahl an Polyedern. In der Tabelle ist die Anzahl der Ecken der Anzahl der verschiedenen Typen von Polyedern zugeordnet. Man erkennt, dass die Anzahl der Typen rapide ansteigt. So gibt es nur ein einziges Polyeder mit vier Ecken: das Tetraeder. Verteilt man nämlich vier Punkte im Raum, so liegen sie entweder alle auf einer Ebene, oder man erhält immer eine Pyramide über einem Dreieck.
| Ecken | Polyeder |
| 4 | 1 |
| 5 | 2 |
| 6 | 7 |
| 7 | 34 |
| 8 | 257 |
| 9 | 2.606 |
| 10 | 32.300 |
| 11 | 440.564 |
| 12 | 6.384.634 |
| 13 | 96.262.938 |
| 14 | 1.496.225.352 |
| 15 | 23.833.988.129 |
| 16 | 387.591.510.244 |
| 17 | 6.415.851.530.241 |
| 18 | 107.854.282.197.058 |
| 19 | ??? |
Für fünf Ecken gibt es nur zwei Möglichkeiten: die Pyramide über einem Viereck, wenn vier der fünf Punkte auf einer Ebene liegen, oder die Doppelpyramide über einem Dreieck. Die sieben verschiedenen Typen von 6-eckigen Polyedern zu finden, wird dann schon langsam komplizierter.
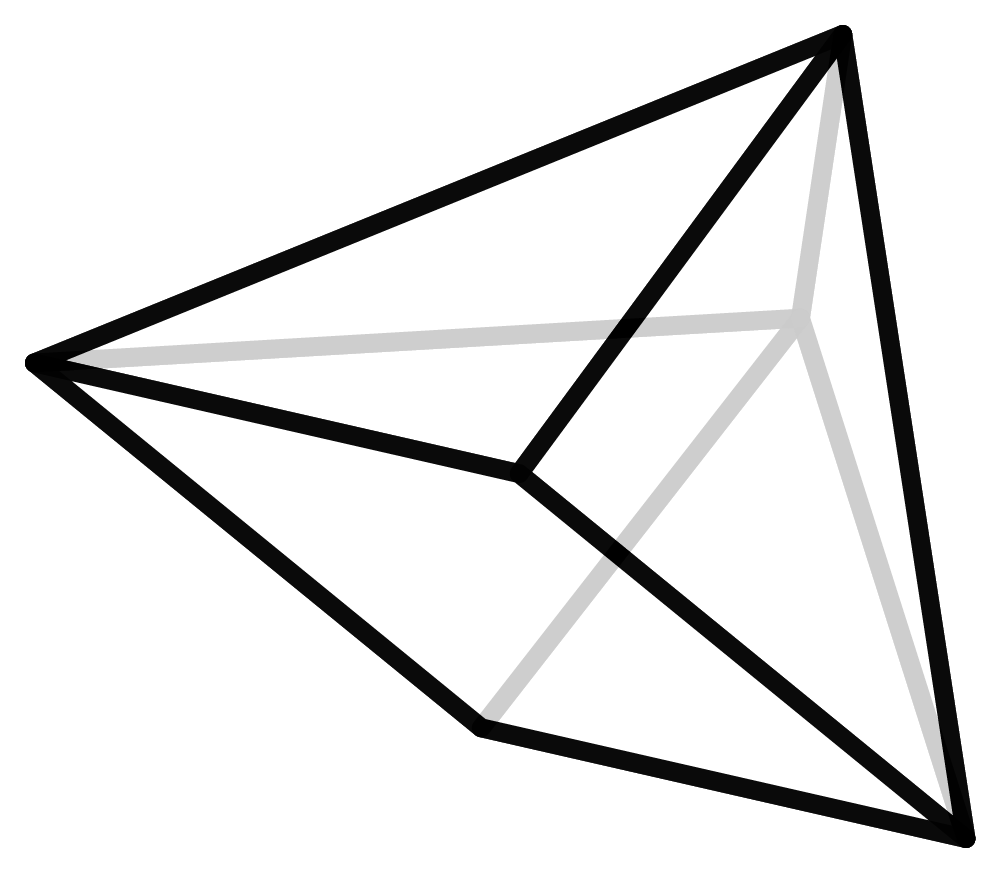

Um herauszufinden, wie viele Polyeder einer gewissen Anzahl es tatsächlich gibt, müssen wir sie auflisten. Dazu müssen alle erstellt werden. Woher aber weiß man, dass diese Liste vollständig ist und kein Polyeder doppelt vorkommt? In der Geometrie gibt es den Satz von Steinitz, der besagt, dass jedes Polyeder eindeutig einem Graphen mit einer bestimmten Eigenschaft zugeordnet werden kann. (Hier geht es um die Protagonisten aus der Graphentheorie und nicht diejenigen, die in Koordinatensystemen zu Hause sind.) Diese Graphen sind mathematisch leichter zu fassen und damit abzuzählen. Doch auch hierfür benötigt man einen Computer, da die Zahlen schnell sehr groß werden. Die Anzahl der sieben- und achteckigen Polyeder, nämlich 34 bzw. 257 Stück, wurden bereits im Jahre 1899 gefunden. Bis zur Entdeckung der 2606 neuneckigen Polyeder im Jahre 1969 war die Erfindung des Computers notwendig.
Dimensionen
In der Mathematik gibt es viele Möglichkeiten Dimensionen zu interpretieren. Der zugänglichste ist, sich die Dimensionen als Variablen vorzustellen. Einen Apfelkuchen zum Beispiel, der aus 6 Zutaten, sagen wir: Mehl, Butter, Zucker, Eiern, Backpulver und Äpfeln besteht, kann man als sechsdimensionales Objekt verstehen.
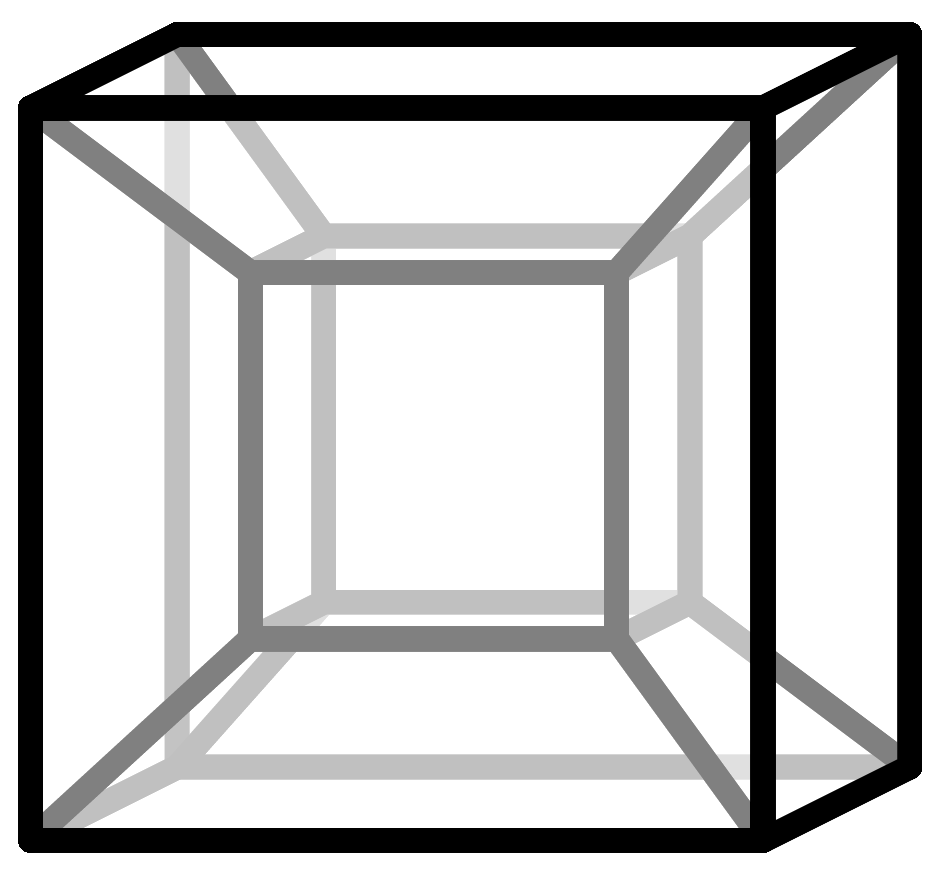
Durch das Betrachten von Fotos und Filmen, die ja immer eine Darstellung unserer dreidimensionalen Welt in einem zweidimensionalen Medium sind, sind wir es gewohnt eine Dimension mehr zu sehen. Den Vorgang des Abbildens einer höheren Dimension in eine niedrigere, also wenn man ein Foto, dass ja zweidimensional ist, von der dreidimensionalen Welt macht, nennt man in der Mathematik Projektion. Da es leider nicht möglich ist, den vierdimensionalen Raum im uns umgebenden dreidimensionalen Raum wirklich unterzubringen, müssen wir uns mit Projektionen behelfen.
Betrachtet man zum Beispiel den Würfel, so bestehen seine Seitenflächen aus Quadraten. Ein Quadrat kann man sich, da alle seine Kanten gleich lang sind, als einen zweidimensionalen Würfel vorstellen. Die Seiten des dreidimensionalen Würfels sind demnach zweidimensionale Würfel. Dieser Zusammenhang lässt sich auch auf höhere Dimensionen übertragen. Die Seitenflächen eines vierdimensionalen Würfels bestehen dann aus dreidimensionalen Würfeln. Es entsteht ein sogenannter Tesserakt. Hier ist ein Link zu einem Video (mit Untertiteln) in dem dieser Zusammenhang noch einmal graphisch visualisiert wird.
Konvex/Konvexität
Wenn wir von Polyedern sprechen, setzen wir stillschweigend voraus, dass es sich um konvexe Polyeder handelt. Konvex bedeutet, dass es keine Einbuchtungen nach innen, Aushöhlungen oder Löcher gibt. Die mathematisch korrekte Definition von Konvexität besagt, dass es für je zwei Punkte, die innerhalb einer Menge liegen auch ihre Verbindungsstrecke komplett innerhalb der Menge liegen muss.
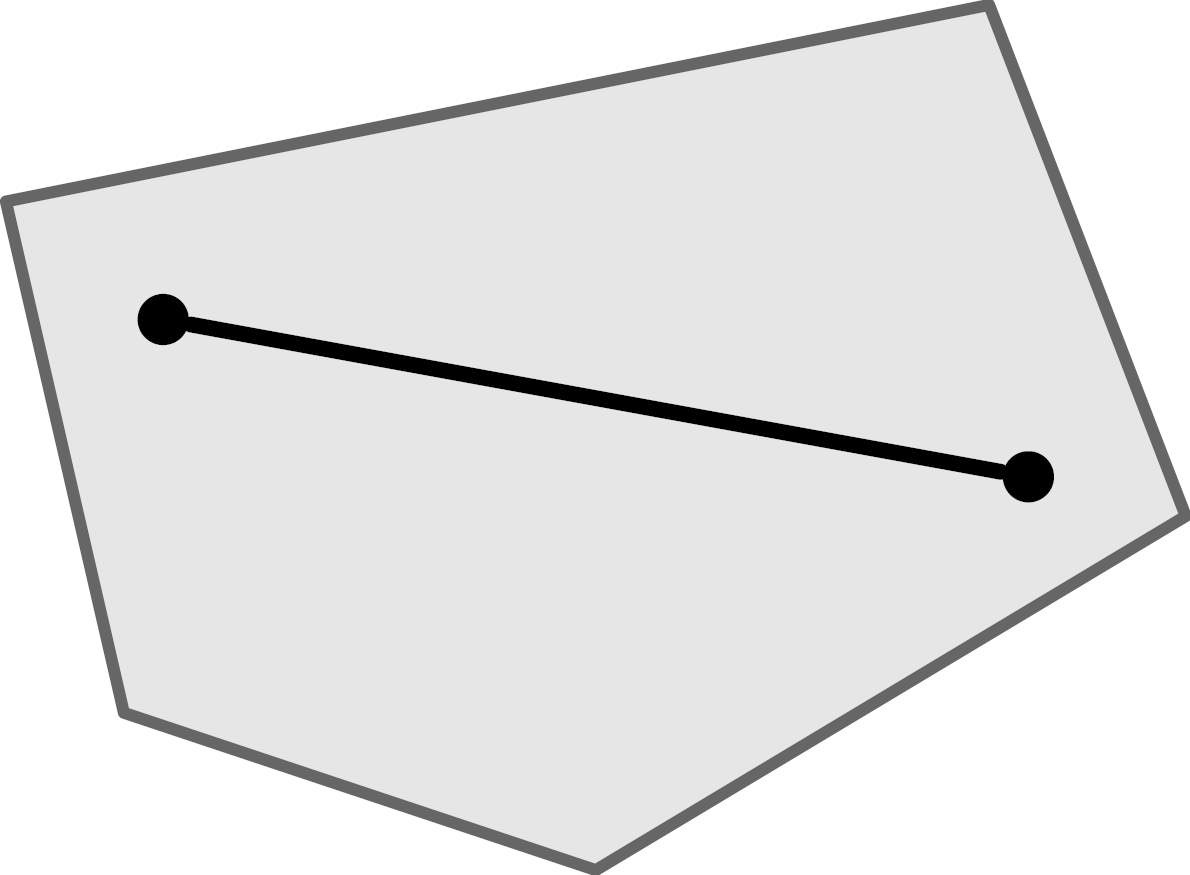
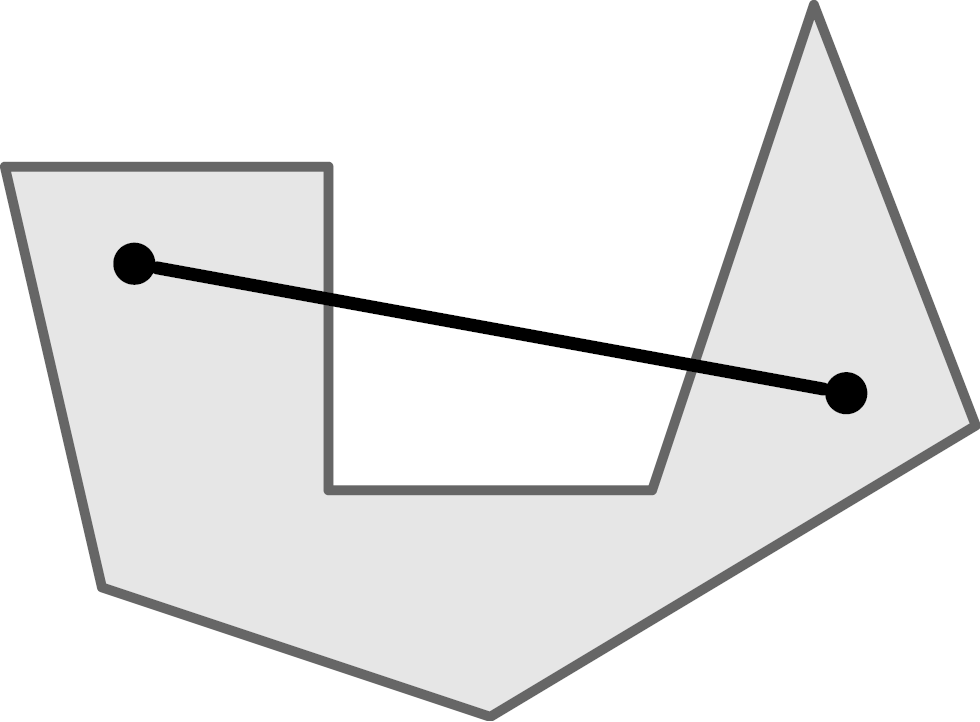
Links ein konvexes Objekt, rechts ein Objekt, das nicht konvex ist.
Kombinatorischer Typ
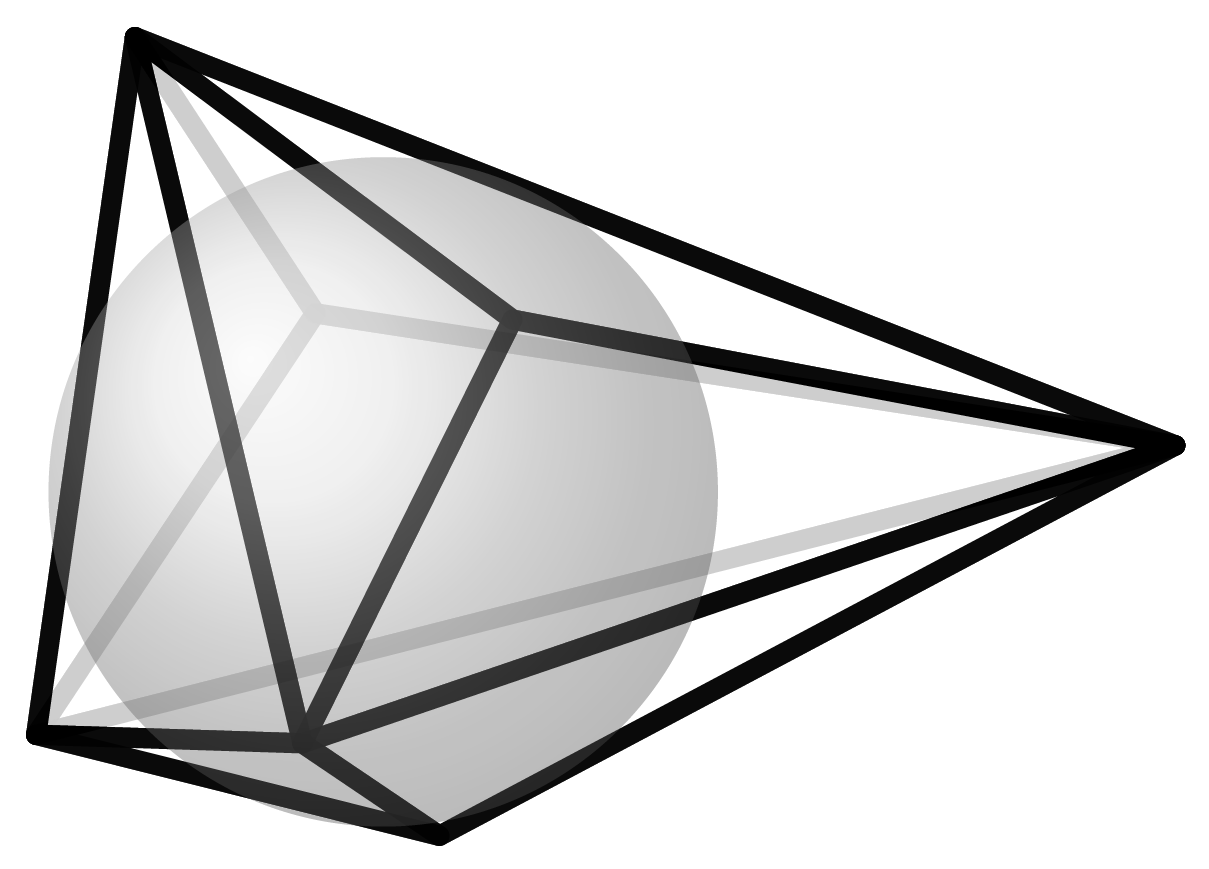
Jedes Polyeder kann auf verschiedene Arten geometrisch realisiert werden. Es kann groß oder klein sein, seine Form kann sich verändern, solange die Struktur der Ecken, Kanten und Flächen dieselbe bleibt. Diese Struktur, das Zusammentreffen der Kanten in den Ecken und die Anzahl der Ecken, die zu einer Fläche gehören, nennt man den kombinatorischen Typ eines Polyeders. Wir nennen zwei Polyeder kombinatorisch äquivalent, wenn sie denselben kombinatorischen Typ besitzen. d. h. wenn man die Ecken eindeutig einander zuordnen kann, so dass, wenn zwei Ecken in einem Polyeder durch eine Kante verbunden sind, auch die Ecken im anderen Polyeder eine gemeinsame Kante besitzen. Jedes Polyeder hat unendlich viele verschiedene geometrische Realisierungen. Wenn Du Dir hier auf Polytopia.eu ein Polyeder aussuchst, adoptierst du gleich den ganzen kombinatorischen Typ. Das bedeutet, dass du eigentlich gleich unendlich viele Polyeder adoptiert hast. Damit es aber nicht ganz so unübersichtlich ist, und du auch irgendwann mal mit dem Modellbauen fertig wirst, haben wir uns auf eine eindeutige Realisierung der Polyeder festgelegt. Es sind die sogenannten Koebe-Andreev-Thurston-Realisierungen der Polyeder. Ihre Besonderheit ist, dass im Inneren des Polyeders eine Kugel einbeschrieben ist, die jede der Kanten des Polyeders an genau einem Punkt berührt. Insbesondere beinhaltet jede Seitenfläche damit einen Kreis, der die Kanten genau einmal sanft berührt.

f-Vektor
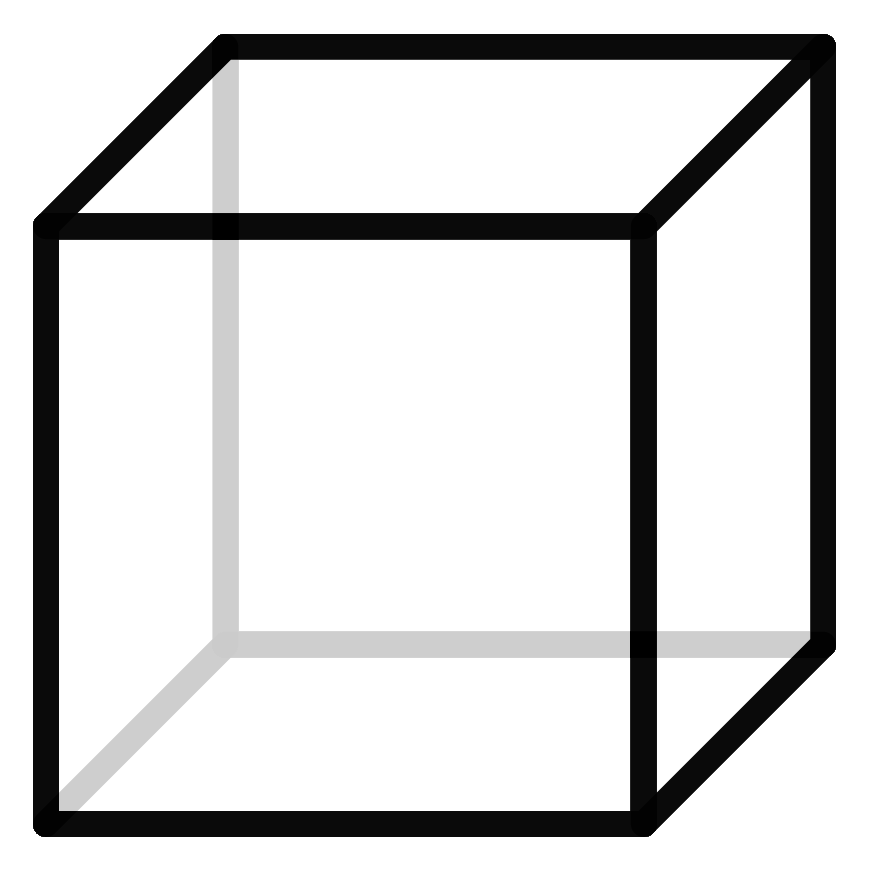
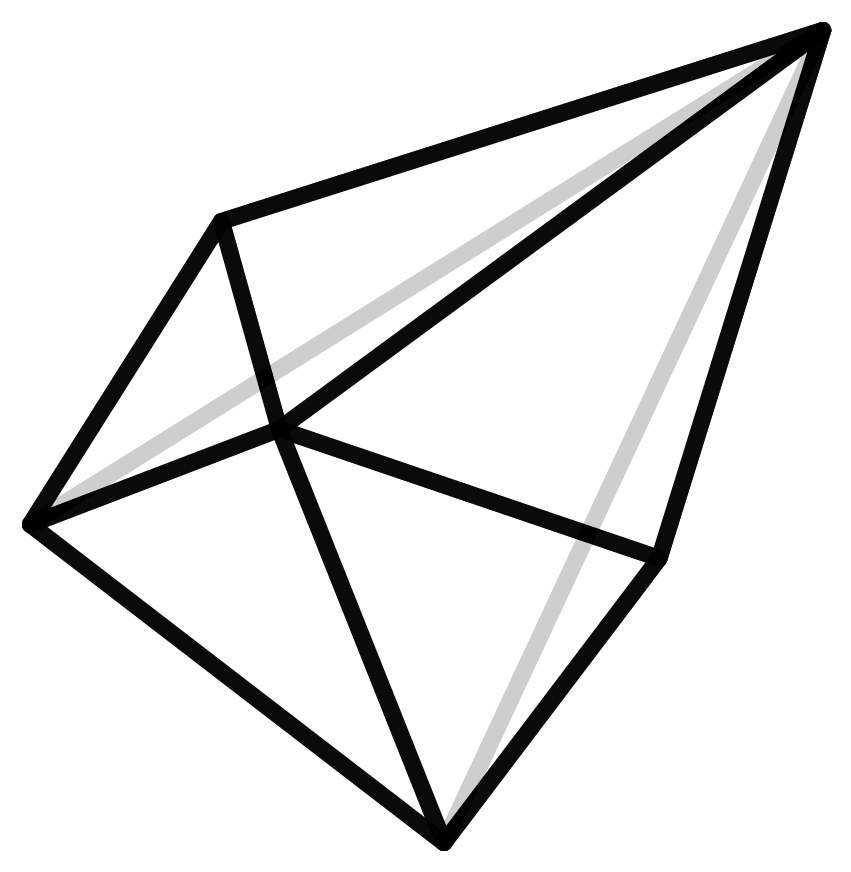
Der f-Vektor eines Polyeders gibt an, wie viele Ecken, Kanten und Seitenflächen es besitzt. Ein Vektor ist in diesem Fall keine geometrische Größe, sondern nur die Art und Weise der Darstellung dieser Zahlen. Der Würfel besteht aus 8 Ecken, 12 Kanten und 6 Seitenflächen und hat somit den f-Vektor (8,12,6). Durch diesen Vektor sind die Polyeder allerdings nicht eindeutig bestimmt. Es kann andere Polyeder mit demselben f-Vektor geben, die eine völlig andere Struktur haben. Diese Polyeder nennen wir auch Geschwister.

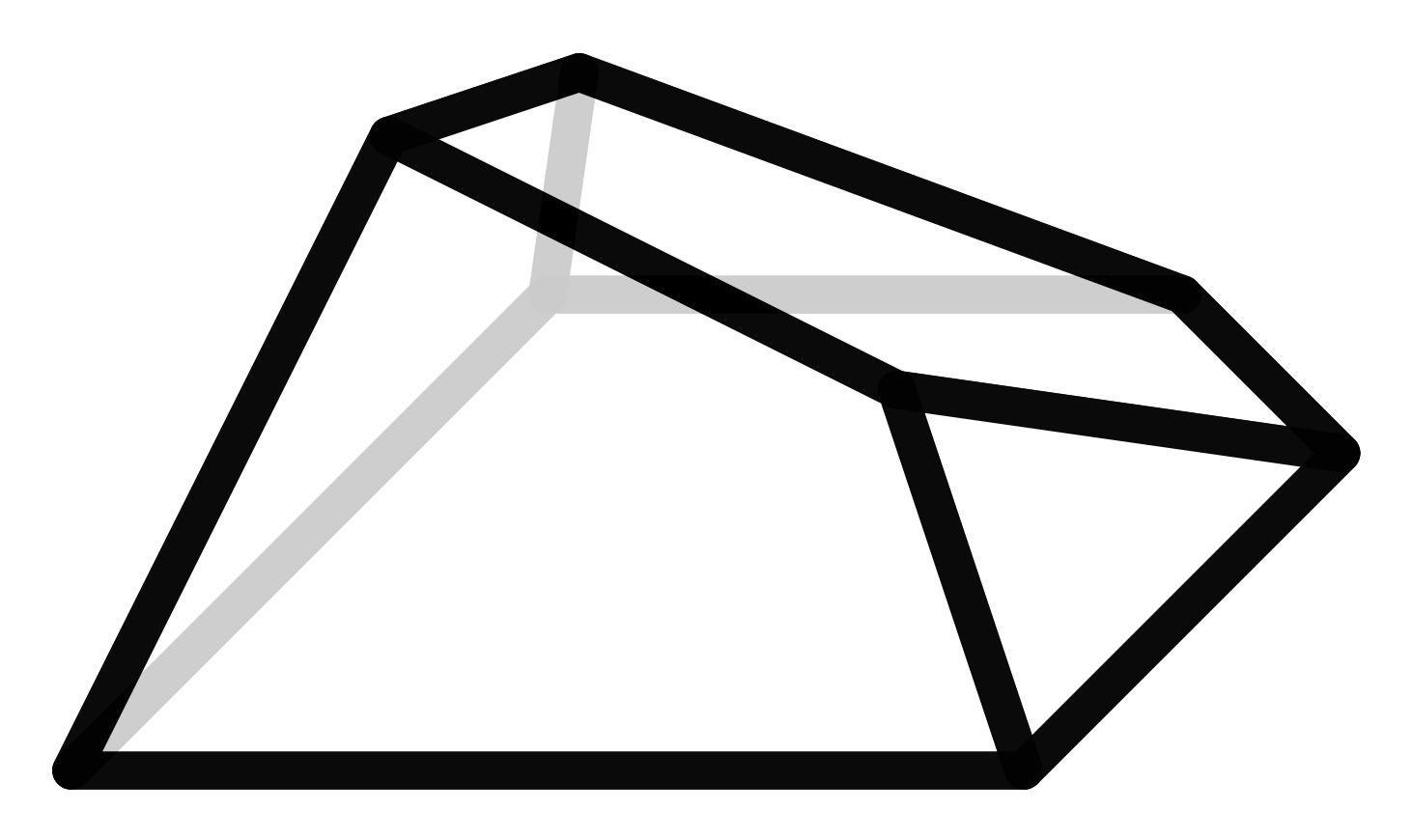
Hier sehen wir den Würfel und seine Schwester, die ebenfalls 6 Seitenflächen, 12 Kanten und 8 Ecken besitzt, jedoch eine ganz andere Struktur hat als der Würfel.
Mathematische Modelle
Mathematische Modelle und deren Bau spielten in der wissenschaftlichen Mathematik lange eine wichtige Rolle. Zum einen gab es einfach keine andere Möglichkeit, um sich zu einer Anschauung im Raum zu verhelfen. Natürlich kann man dreidimensionale Modelle auch zeichnen, dann erhält man aber immer nur eine Projektion des Raumes in die Ebene, wie bei einem Foto. Bei diesen macht uns das Erkennen des Raumes keine Probleme, weil wir ja wissen, dass ein Tisch meistens rechtwinklig ist. Sehen wir einen perspektivisch verzerrten Tisch auf einem Foto, so wissen wir intuitiv, dass er eigentlich rechtwinklig ist. Anders ist das natürlich, wenn man überhaupt erst mal begreifen möchte, welche Struktur ein geometrisches Objekt besitzt. Um z. B. eine Symmetrieachse zu erkennen, ist es sehr hilfreich einen Körper tatsächlich in der Hand halten und drehen zu können.
Modelle dienten jedoch nicht nur dem eigenen Erkenntnisgewinn, sondern auch der Wissensvermittlung. Um die eigene Forschung anderen zugänglich zu machen, brauchten Mathematikerinnen und Mathematiker eine Möglichkeit zur Visualisierung. Heutzutage wird dies vor allem mit dem Computer gemacht. Es gibt zahlreiche Möglichkeiten mathematische und geometrische Graphiken zu erzeugen. Durch Rotation eines Modells wird auch dem Problem der Einschränkung auf den flachen Bildschirm entgegengewirkt.
Dürers Vermutung
Obwohl sich schon seit der Antike Mathematikerinnen und Mathematiker mit Polyedern beschäftigen, ist noch lange nicht alles über sie bekannt. Ein „schönes“, weil leicht verständliches und doch bislang ungelöstes Problem ist die sogenannte Dürer’sche Vermutung. Der Maler Albrecht Dürer hat sich einige Jahre lang intensiv mit Mathematik beschäftigt. Auf ihn geht auch das Konzept des Polyedernetzes zurück. In seinem Buch „Underweysung der Messung, mit dem Zirckel und Richtscheyt“ zeichnete er Netze von verschiedenen Polyedern.
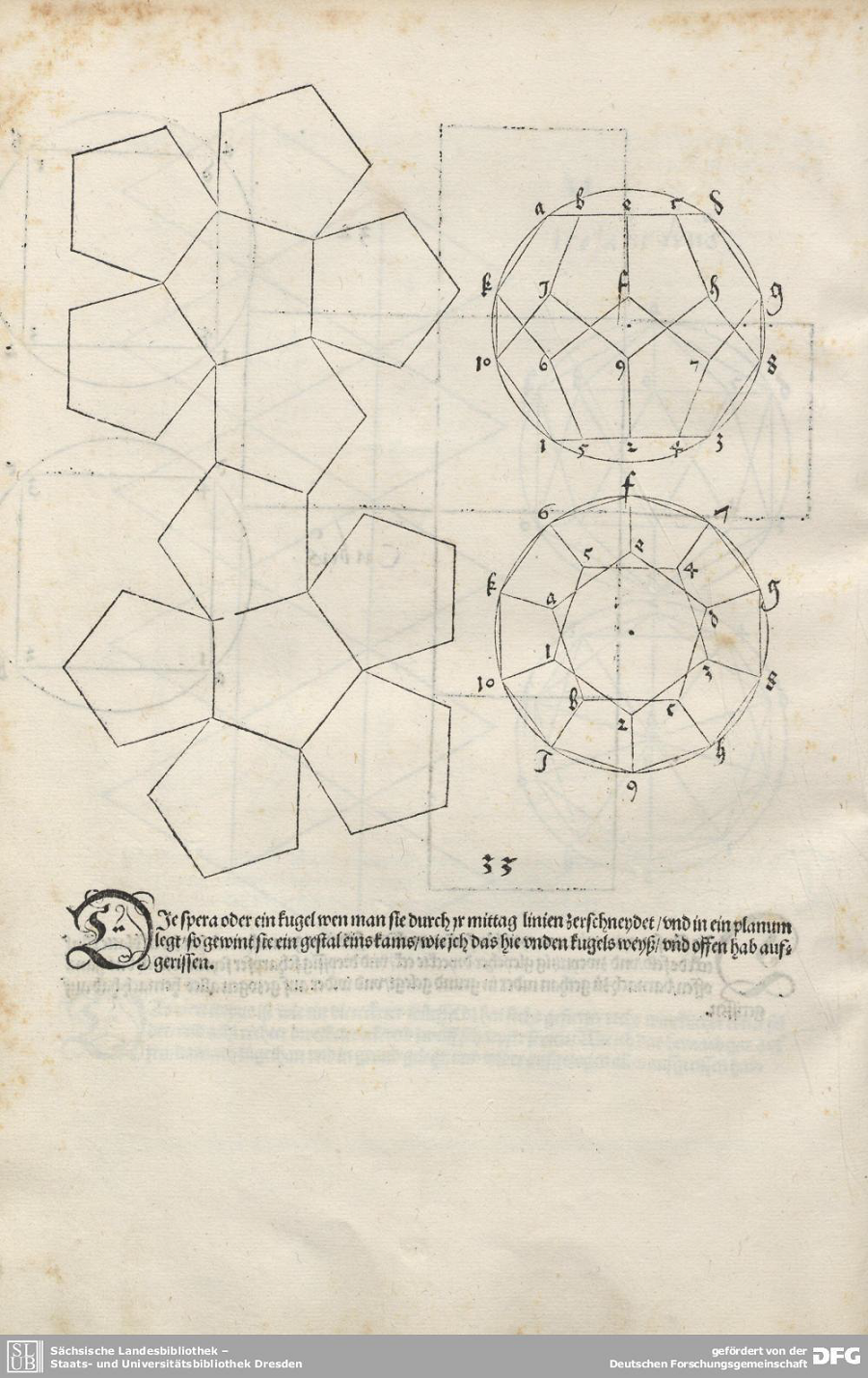
Ein Polyedernetz entsteht, indem man das Polyeder als leere Hülle betrachtet, die man nun entlang seiner Kanten so aufschneidet, dass sie zusammenhängend bleibt, aber flach aufgeklappt werden kann. Auf diese Weise entsteht eine Art Bastelbogen für das Polyeder. Die Frage hinter Dürers Vermutung lautet nun, ob dies mit jedem Polyeder so möglich ist, dass sich die Seitenflächen in der Ebene nicht überschneiden. Besitzt also jedes Polyeder einen Bastelbogen?
Bis heute haben sich viele Mathematikerinnen und Mathematiker mit diesem Problem beschäftigt. Es gibt erste Zwischenergebnisse. Zum Bespiel ist bekannt, dass man jedes beliebige Polyeder so in die Länge ziehen kann, dass es dann überschneidungsfrei aufgeklappt werden kann (s. https://arxiv.org/pdf/1305.3231.pdf). Dadurch ändert sich zwar die geometrische Realisierung des Polyeders, nicht aber seine Struktur. Auf der anderen Seite ist das Tetraeder das einzige Polyeder, für das wir wirklich wissen, dass es immer aufgeklappt werden kann, egal wie sehr es verzerrt ist.
Da wir die Polyedernetze und somit die Bastelbögen der Polyeder automatisch generiert haben, ist es möglich, dass das Netz deines adoptierten Polyeders sich überschneidet und somit nicht ausgeschnitten werden kann. Sollte das bei deinem Polyeder so sein: Schreib uns eine E-Mail!
Geschwister
Wir nennen Polyeder Geschwister, wenn sie dieselbe Anzahl von Ecken, Kanten und Seitenflächen, also denselben f-Vektor, haben. Wie menschliche Geschwister sehen sich manche sehr ähnlich, andere wiederum haben eine völlig andere Form. Der Würfel besteht aus 8 Ecken, 12 Kanten und 6 Seitenflächen. Diese Zahlen definieren ihn also nicht eindeutig, denn es gibt auch andere Polyeder mit diesem f-Vektor, die eine völlig andere Struktur haben.
Geschwister:Cookie, Kaichen, Tigger, Vizzlokaeder, Recoleta, MaWi, stiebe_Rieß-mit_Mem, Polytrinchen, 222Polytopia222, Ploxlinueder, My Loveâ¤ï¸, Walli, Hi Herr Rosenbaum 👋ðŸ», Sharko, dominikanischerEder, LA2007, polywona, Chline Flizer, Nubia, Sheru, . . .
Janne, ChaosAnanas, Flopsy, David polyface, Hemil von Tatezi, little shard, Leopold, Link, Rondwick von der Ecke, Totsulo, DoubleP, Paulator, Joschka, Norideder, Fußballl auf die 1, Karolina, Крали Момчо, Rainbow, Lila, maryeder, akunandaba, Wincent , Sybille, Daz, Doctor Who, Luna Angel darkness, Greenhorn, Annyeder , Weaselstein, Manuhedron, lillyeder, Friedlinde, Günter, Janlovedebussy, Paulchen, Misha_03_27, Sinan, Spitzi, NovemÅ«ndÄ“vÄ«gintÄ«duodecim, Annette, William, Isaeder, Marcohedron, Coconut , Septimiuscäsus, Victorhedron, Polyto, CC:Elii , Morscheder, Herta, Mummler, Hope, MiA ðŸ’â¤, Queen, Adelheid, Kazhaam, Kalón, Ruggeheimer Polyboi, Holieder, SCHLANGI, Irene, Lumpi Walter, Eddah, 10-2-dodecatallship, Lulueder, Team , Marko, Laser, Tiberius, Malius, TomasCat, BoB der B1ob, Langspitz, ΠητεÏ, the world, Joshi, Mathi, Dasha, Auflauf, Fritz, Meow-eder, On top of the house, Bilbotope, Wolken-Kratzscherbe, Panopticon, Jaya, Lea6, Tapir, Mathilde, Muutz von Plym, Achterdeck, Häuptling Mahühnchen, Poly, Monaeder Otytope, Fedra La Poliedra, The Nonohedron, Otto Fritz Müller, Ederhard Polmann, Paulino22, Herz Darnok, Ludwig II, Funkel, Wolf, Meister Eder, Chicken-Man, Norwegese, Bépy, Frida, simetri-free, Polkopf, Auroraeder, Lea, das Polyeder, Mori, Paldadobey, Long Boy, ABSTECHER, Haariger Harald💙, Kyubii, kiki, KIKI1, Kobobieder, StarlordOne, Ziellinder, Polligkeit, Long point, sockenpaket, Neko lolis are the best, Pollopholus, Sabrina, Fini, Liane , Jasper alexander müller, Monika, Ditrikus, Schlauphinchen, Mr Richards, Orakel-Lay, Duodecim ahlgrimm polyhedra, Sternenkreuzer, polyhedrus judithus, Sternenschiff, Fred, YouNotUs, Mexodor, Polynikolon, Edda, Ingo , Elo, Kleiner Fuchs, t-bone [EGE], Polyphemi, Pointy Von Longshnoot, Erik, Vektor, Baby Princess, Hädäck, , Estrelinha, nilsieder, AlinaSilverberg , KastenStahl_EGE, Banani , Jakob, Trempton, Julian, Georgia, Katie-gon, Ilay, Sugarstar, Dori, solver, kirari, Klausimyriadoeder, Trinchen, Polysusi, Luise, FMS, Lars, Kisondra, Bastibububär, ich hasse pink, Roskofiedro, Cecilyeder, Veronika, FloRotheder, crystal, RoffelXD, Eckbert, Johnny, Anne Elisabet, Konstantin, FireGirl , Thomasin Thorsteensis Walterus, Theodor, Leonardo , Polina, bauleck, Ranja007, Spitzer Batzen, Cäru Litaeder, Polymaxi, Stick, Symmetrielya, paupel, Odette, Samuel, Rein'lyed, Jomali, Edgareder, Nyander, Milica, Schneck, Roxy, Dennis, Kiziro🎪, Ulvu aus Krefeld, Füchschen, Titus, Berni, Anna Naklab, Jungchen 42, Karri, Sekitope, der Fink, Henrie , Atheneder, Wolfgang_1241, allEcksa, Hier könnte Werbung stehen!, Satori, Lucaso Eder 5b, Dilithium, Arne, Polyerine, Henrik, coco, Pfeiffa, Maya Rose 1, Langwaldscher Körper, Klingon Empire, Peter L., Josephine, Hildegard, Lisas Morgenstern, Soul, Fluffi, GWIAZDA, Zelt im Sturm, Sherry Zhang, Pearl, Jürgen-Polyeder, manseohedron, Jones, Gabi, Lionel Pessi, Quicksi, Oscar, Odontoleon, КарлÑон который , Kerim2, Luca, Meisel, ARABRAB, polyhedrus katharinus, Carlos Stinker, Anne, Elisabet, Croissant, Parya, Bananoeder, NiNo, Testi, Falstaff, G@lc2008, Polypia, Jannaeder, Marie Super Girl, ich habe keinen Namen, Polygünther, Steinscher Polyeder, Sia, CSC MARBURG, Shooky, Society, JochenThorstenUwe, Taj, Rürü, Zwölfseitiger Kressendrache, Türk , Louis Vuitton quatorze, AndyPandy, Heribert , Jakartoffel, Mamaeder, H8, redeyloP, Theti, Bunti-Eder, Tildette, falkholger, Mümeleder, Pauli, Jasper, Poly Keren, Gelaschatzi, Schlowgard, Galahad, Polylein, Luedchen , Diamond, Marlene, Mbali , 4 R3N4T3, Andantehedron, Peter Paker, Setamieder, Valieder, Pollyhedron!, Raineder, Martha, Poppy, Shinobu, Josh Hutcherson 😈, Cosma , Cooli, Rutestand, ABFAHRT , Mouna, Ultraeder, Pommes, Corallus Maximus, nölly_das coole polyeder, Quem, Jifancon, Maestro Rüdiger III., ❤️ MaoMao ❤️, POLY_007, Valivalou, charly, Lua, Karli Lu, Richhart, Orlaith die süßeste, Dobby, Paulajohannagon, Christoph der Sachse, Le Monsieur 235Hellhundonit, Glüx-Polyeder, Auf Zack, Hendrix, Pinki_winki, Harry B., Polywang, Sympholy, Magnus, Fridolin , SERVUS , Frohe Weihnachten Bebi, Albert Schur, Teapot, Adrian, Claudias, Mistery Rainbow, PEMtradeder, Jaaht Corp., Sunny-Eder, Juweloeder, Orgon, ball, Claudio, karamboeder, Christine, Yunus, Dollideder, Horst <3, Maggie, Eure Flauschigkeit Sonja, Qualloeder, Eleeder, Frankel, Ikaruzz, Gregory, Life, Helmoldeder, Vampirkatze, Cm2chav, Maximus Elprimu, Raibieder, Jef, doolyreader, 💎, Mond, Matjeder, Carter, Pina von Polytopia, Timy Eder 5b Silverberg, Piet, Dhihedral-Inradialer-CoKite, Habibi, Dr. P. Eder, Carl-Blessing-Eder, Kite-like, Pauljester, Anahita, polypi, Pikaã¡ã‚ƒã‚“, Lea-Marie, Sharif, Shaja, Christiana, Amer, Dilfie, Sophia ;-), Qual der Wal, Apollo 21.05, SVVhisky, Brõckereder, Frankenstein, JO, Thorben Henrdyx, Jalasaid, Qwerty, Eckerhard, Elena, Jaid, Dogedron, Quorzel, Quaderus, matt eagle leberwurst, Thorben, Mike Winkler Silvester 2018, Dia die Königin, Twelfie, Chimpanzo, The Rock, Polya, Pia-Polyeder, Rous, Polyg Lotti, ReubieDoobieHedron, Messerschmidtoeder, Anokata, Diamantos, Geometria, Luda, Diamanticus, Lobster SCM, Kiragon, Almuths Equilibrium, Hoplit, Luna, aihpos inele resalg , Lenoire, Geschwisterchen 900281, Geschwisterchen 900283, Geschwisterchen 900403, Geschwisterchen 900592, Geschwisterchen 900597, Geschwisterchen 900649, Geschwisterchen 900654, Geschwisterchen 900661, Geschwisterchen 900677, Geschwisterchen 900693, Geschwisterchen 900708, Geschwisterchen 900713, Geschwisterchen 900756, Geschwisterchen 900775, Geschwisterchen 900797, Geschwisterchen 900800, Geschwisterchen 900807, Geschwisterchen 900809, Geschwisterchen 900811, Geschwisterchen 900815, Geschwisterchen 900875, Geschwisterchen 900887, Geschwisterchen 900957, Geschwisterchen 900961, Geschwisterchen 901039, Geschwisterchen 901043, Geschwisterchen 901052, Geschwisterchen 901061, Geschwisterchen 901101, Geschwisterchen 901196, Geschwisterchen 901219, Geschwisterchen 901237, Geschwisterchen 901247, Geschwisterchen 901267, Geschwisterchen 901277, Geschwisterchen 901278, Geschwisterchen 901285, Geschwisterchen 901287, Geschwisterchen 901300, Geschwisterchen 901317, Geschwisterchen 901346, Geschwisterchen 901348, Geschwisterchen 901367, Geschwisterchen 901399, Geschwisterchen 901447, Geschwisterchen 901485, Geschwisterchen 901514, Geschwisterchen 901535, Geschwisterchen 901543, Geschwisterchen 901563, Geschwisterchen 901571, Geschwisterchen 901577, Geschwisterchen 901600, Geschwisterchen 901617, Geschwisterchen 901623, Geschwisterchen 901625, Geschwisterchen 901637, Geschwisterchen 901719, Geschwisterchen 901724, Geschwisterchen 901735, Geschwisterchen 901772, Geschwisterchen 901775, Geschwisterchen 901782, Geschwisterchen 901878, Geschwisterchen 901896, Geschwisterchen 901963, Geschwisterchen 901965, Geschwisterchen 901973, Geschwisterchen 901979, Geschwisterchen 901995, Geschwisterchen 902005, Geschwisterchen 902039, Geschwisterchen 902047, Geschwisterchen 902138, Geschwisterchen 902155, Geschwisterchen 902159, Geschwisterchen 902318, Geschwisterchen 902326, Geschwisterchen 902341, Geschwisterchen 902365, Geschwisterchen 902385, Geschwisterchen 902211, Geschwisterchen 902213, Geschwisterchen 902215,
ausblenden
Anwendungsgebiete von Polyedern
Aus der Perspektive der reinen Mathematik sind Polyeder vor allem schön und interessant und ihre Erforschung bedarf keiner weiteren Rechtfertigung. Dennoch kann man auch hier natürlich die Frage stellen, die fast genauso alt ist wie die Mathematik selber: Und wofür braucht man das eigentlich?
Ein wichtiges Anwendungsgebiet von Polyedern ist die Lineare Optimierung. Es handelt sich hierbei um eine Methode, die unter anderem in der Wirtschaft häufig verwendet wird, um Entscheidungen zu treffen, die von vielen Faktoren abhängen.
Im öffentlichen Nahverkehr ist das Planen der Netzlinien und Erstellen der Fahrpläne ein solches Problem. Viele Faktoren müssen berücksichtigt werden, wie Ankunfts-, Abfahrts- und Wegzeiten, Netzauslastung, Unterhaltskosten, Anzahl der zu befördernden Personen und so weiter. Die Verkehrsplaner müssen versuchen, den Verkehr flüssig zu gestalten und dabei die Kosten so gering wie möglich zu halten. Aus diesen Variablen entsteht ein System aus linearen Ungleichungen, deren Lösungsmenge ein Polytop bildet. Die optimalen Lösungen liegen in den Eckpunkten dieses Polytops. Um den effektivsten Fahrplan zu erstellen, müssen also die Eckpunkte des Polytops gefunden werden.
Wie kommen eigentlich die Namen von Mathematischen Objekten zustande?
Das Dreieck heißt „Dreieck“, weil es drei Ecken hat. Es hat aber auch drei Kanten. Unter einem Dreikant stellt man sich allerdings eher ein Werkzeug vor. Es reicht also nicht aus, dass der Name scheinbar schon eine Definition ist. Es ist zudem notwendig, dass der Name auch benutzt wird, damit sich seine Bedeutung einschleift.
Wie steht es aber mit mathematischen Objekten, die nach Mathematikerinnen und Mathematikern benannt wurden? An dieser Stelle kann man natürlich einwenden, dass wohl viel mehr Mathematiker Namenspatronen von Sätzen oder Konzepten sind als Mathematikerinnen. Um hervorzuheben, dass es sie aber doch gibt, sind an dieser Stelle sowohl die Noether-Ringe (nach Emmy Noether) als auch die Versiera der Agnesi (nach Maria Agnesi) zu nennen. Trotzdem besteht hier natürlich Aufholbedarf!
Wie kommt es zu diesen Namenskonventionen? Meistens werden Objekte, die mit einem Namen versehen werden, von anderen Wissenschaftlerinnen und Wissenschaftlern nach ihnen benannt. Das Konzept eines Ringes war ja zum Beispiel schon bekannt. Um dann die Ringe, über die Emmy Noether schrieb, von den allgemeinen unterscheiden zu können, sprach man eben über Noether-Ringe und so bürgerte sich zunächst eine Konvention und später eine Definition ein.
Dürers Vermutung hingegen hat nicht der Maler Albrecht Dürer selber geäußert. Auf ihn gehen allerdings die zugrundeliegenden Polyedernetze zurück. Die Frage selber stellte der Mathematiker G.C. Shephard im Jahr 1975, ohne sie allerdings so zu nennen. Warum dann im Folgenden von Dürers und nicht von Shephards Vermutung gesprochen wurde, darüber kann man nun spekulieren.
Zusammenfassend kann man also sagen, dass es keine Regeln oder Konventionen zur Namensvergabe gibt. Es verhält sich ähnlich wie mit der Vergabe von Spitznamen. Wenn alle wissen, wer oder was gemeint ist, dann bleibt der Name eben bestehen.