Glossar
Polyeder
Polyeder sind geometrische Körper, die aus Ecken, Kanten und ebenen vieleckigen Seitenflächen bestehen. In unserem Projekt beschränken wir uns auf konvexe Polyeder. Das bedeutet, dass alle inneren Winkel kleiner sind als 180°, also dass sie keine Einbuchtungen, Aushöhlungen oder Löcher haben.
Bekannte Beispiele von Polyedern sind der Würfel oder die Pyramide. Aber auch das Prisma oder das Oktaeder sind manchem vielleicht schon einmal begegnet. Es gibt aber noch viel mehr Polyeder.
Eine besonders symmetrische und regelmäßige Klasse von Polyedern sind die platonischen Körper. Die fünf Polyeder bestehen nur aus gleichseitigen Vielecken. Das Tetraeder, das Oktaeder und das Ikosaeder bestehen aus gleichseitigen Dreiecken. In jeder Ecke des Tetraeders treffen drei davon zusammen. Beim Oktaeder sind es vier und beim Ikosaeder fünf. Legt man nun aber sechs gleichseitige Dreiecke in einem Punkt zusammen, so ergibt sich ein Gesamtwinkel von 360°. Damit liegen die Dreiecke flach auf der Ebene und kein Körper entsteht. Ähnlich konstruiert man auch den Würfel, bei dem in jeder Ecke drei Quadrate zusammenstoßen und das Dodekaeder, in dem je drei Fünfecke aneinander treffen. Dieses Vorgehen verwendete auch Euklid, der in seinem Buch „Elemente“ auf diese Weise bewies, dass es keine weiteren Körper mit dieser Eigenschaft geben kann.


Doch nicht nur symmetrische Polyeder sind für Mathematikerinnen und Mathematiker interessant. Oft suchen sie Polyeder (oder eben ihr höherdimensionales Äquivalent, Polytope), die ganz bestimmte Eigenschaften haben. Wir haben Geometerinnen und Geometer (so heißen die Mathematikerinnen und Mathematiker, die sich mit Geometrie beschäftigen) gefragt, welches ihre Lieblingspolyeder sind und warum. Hier sind einige Antworten:
„Wenn man Polyeder als Edelsteine betrachtet, so ist das Assoziaeder (Artikel in Englisch) der Diamant unter den Polyedern. Diamanten bestehen aus einem in der Natur sehr häufig vorkommenden Element: Kohlenstoff. Genauso entsteht das Assoziaeder durch sehr verbreitete Verfahren. Es fasziniert aber dennoch durch seine einzigartige und besondere Struktur – wie eben der Diamant.“ - Jean-Philippe Labbé.
„Mein Lieblingspolyeder ist das Ikosaeder, denn es ist sowohl sehr komplex als auch sehr einfach. Wenn man anfängt gleichseitige Dreiecke aneinander zu kleben, immer fünf Stück an einer Ecke, entsteht zwangsläufig dieses schöne Stück. Wenn ich mich in der Schule gelangweilt habe – auch das ist vorgekommen – habe ich angefangen Ikosaeder an den Rand meiner Hefte zu zeichnen. Manchmal waren sie natürlich nicht so regelmäßig, ich habe mir einen Spaß daraus gemacht, sie wie Gesichter aussehen zu lassen. Ein weiterer Grund für meine Faszination ist, dass man seine 12 Ecken in 3 Vierecke zerlegen kann, die dem goldenen Schnitt entsprechen und wie borromäische Ringe ineinander verschlungen sind.“ - Francisco Santos.

„Das interessanteste Polyeder ist für mich der ‚Miller-Körper‘ (Artikel in Englisch), der auch als ‚Pseudorhombenkuboktaeder‘ oder als ‚verlängerte verdrehte Quadratsdoppelkuppel‘ bezeichnet wird. Zuerst entdeckt wurde er im Jahre 1905 von D.M.Y. Sommerville. Er hat eine bewegte Geschichte des Übersehen-, Entdeckt- und Wiederentdecktwerdens. (Unter anderem auch von J.C.P. Miller, dem es einen seiner Namen verdankt.) Bei näherer Betrachtung entdeckt man eine Verdrehung des scheinbar perfekten Körpers, der seine Schönheit unterstreicht. Zunächst erscheint er sehr klassisch, wie ein Archimedischer Körper. Nach der modernen Definition dieser Körper gehört er dieser Familie aber nicht an. Darum ist das Pseudorhombenkuboktaeder auch eine Erinnerung daran, dass wir in der Mathematik sorgfältig mit Definitionen umgehen müssen und es immer Ausnahmen und Spezialfälle geben kann, die man zunächst nicht bedacht hat.“ - Günter M. Ziegler.
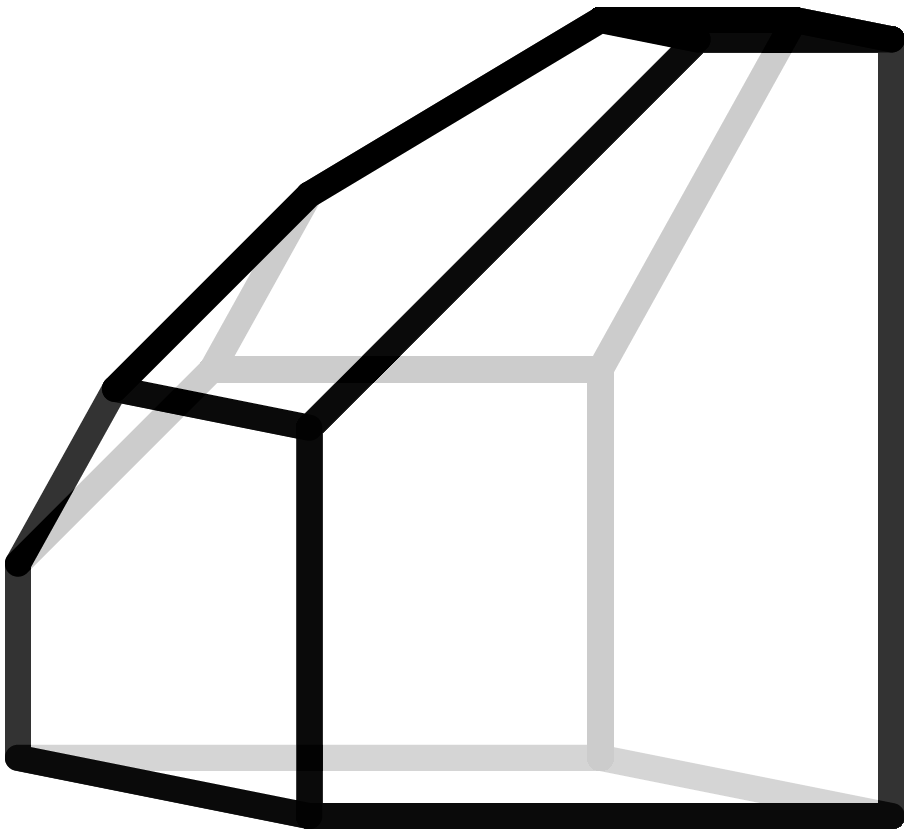
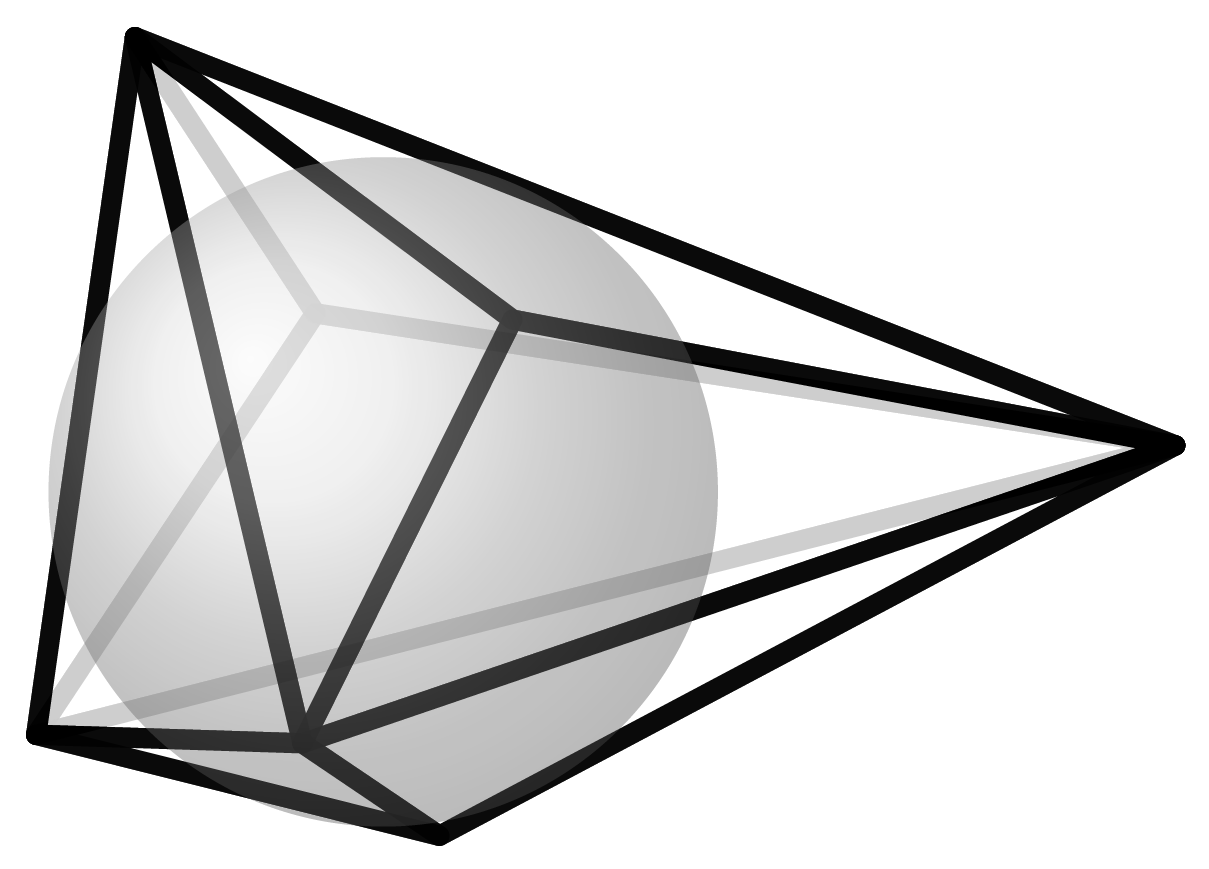
„Die Klasse der Koebe-Polyeder faszinieren mich. Alle ihre Kanten berühren eine Kugel und alle Seitenflächen besitzen einen Innkreis. Die Innkreise von benachbarten Seitenflächen berühren sich in einem Punkt. Es existiert ein expliziter Dualisierungsprozess, mit dem diese diskreten Minimalflächen von Koebe Polyedern generiert werden können. Die dazugehörigen Flächen sind die diskreten P-Schwarz-Flächen und das Koebe-Polyeder ist seine Gauß-Abbildung. Mehr dazu kann man hier nachlesen: A.I. Bobenko, T. Hoffmann, B.A. Springborn, Minimal surfaces from circle patterns: Geometry from combinatorics, Ann. of Math. 164:1 (2006) 231-264) oder nachschauen: (http://discretization.de/en/movies/koebe/).“ - Alexander Bobenko.
Polygon
Ein Polygon, das man umgangssprachlich auch Vieleck nennt, ist ein zweidimensionales Polyeder. Es besteht aus Ecken und Kanten. Die Fläche, die von den Kanten eingegrenzt wird, ist das Polygon selbst.
Eine besondere Klasse bilden die regulären Polygone. Sie bestehen nur aus Kanten gleicher Länge, und alle ihre inneren Winkel sind gleich groß. Das Quadrat, das gleichseitige Dreieck und auch das gleichseitige Fünfeck sind reguläre Polygone. Sie bilden die Bausteine für die Platonischen und Archimedischer Körper.
Polyedernetz
Schneidet man einen hohlen Würfel an ausreichend vielen Kanten auf und faltet ihn dann flach auf die Ebene auf, so entsteht ein Würfelnetz. Zeichnet man dieses Netz auf Papier oder Pappe, so entsteht ein Bastelbogen, den man ausschneiden und zu einem Würfel zusammenkleben kann. Diese Methode funktioniert natürlich auch für alle anderen Polyeder. In unserem Projekt nutzen wir genau diese Bögen, um die Modelle zu bauen. Das Polyeder wird an den Kanten aufgeschnitten und ausgeklappt. Diesen Vorgang haben wir mit dem Computer simuliert und auf diese Weise automatisch die Polyedernetze erstellt.
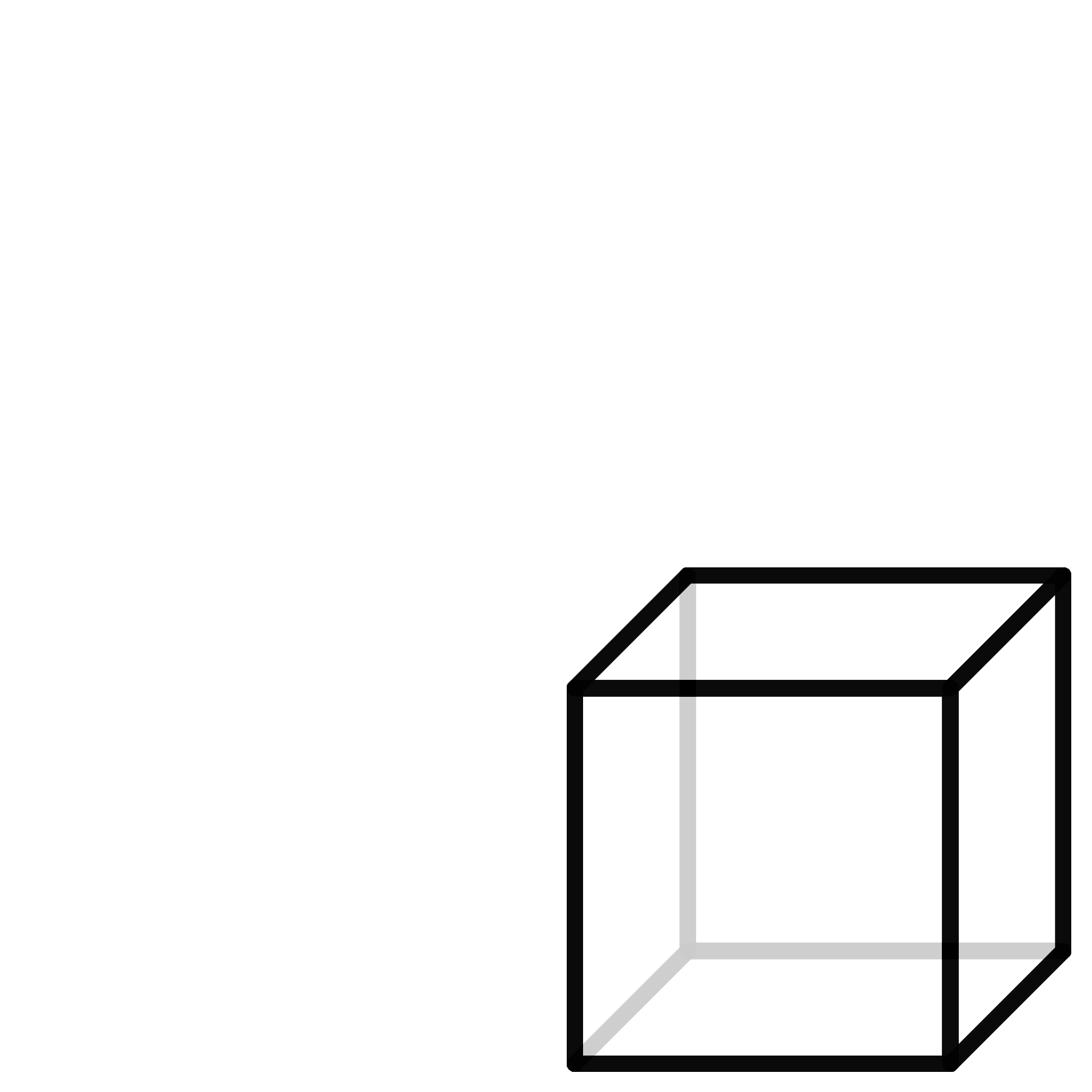
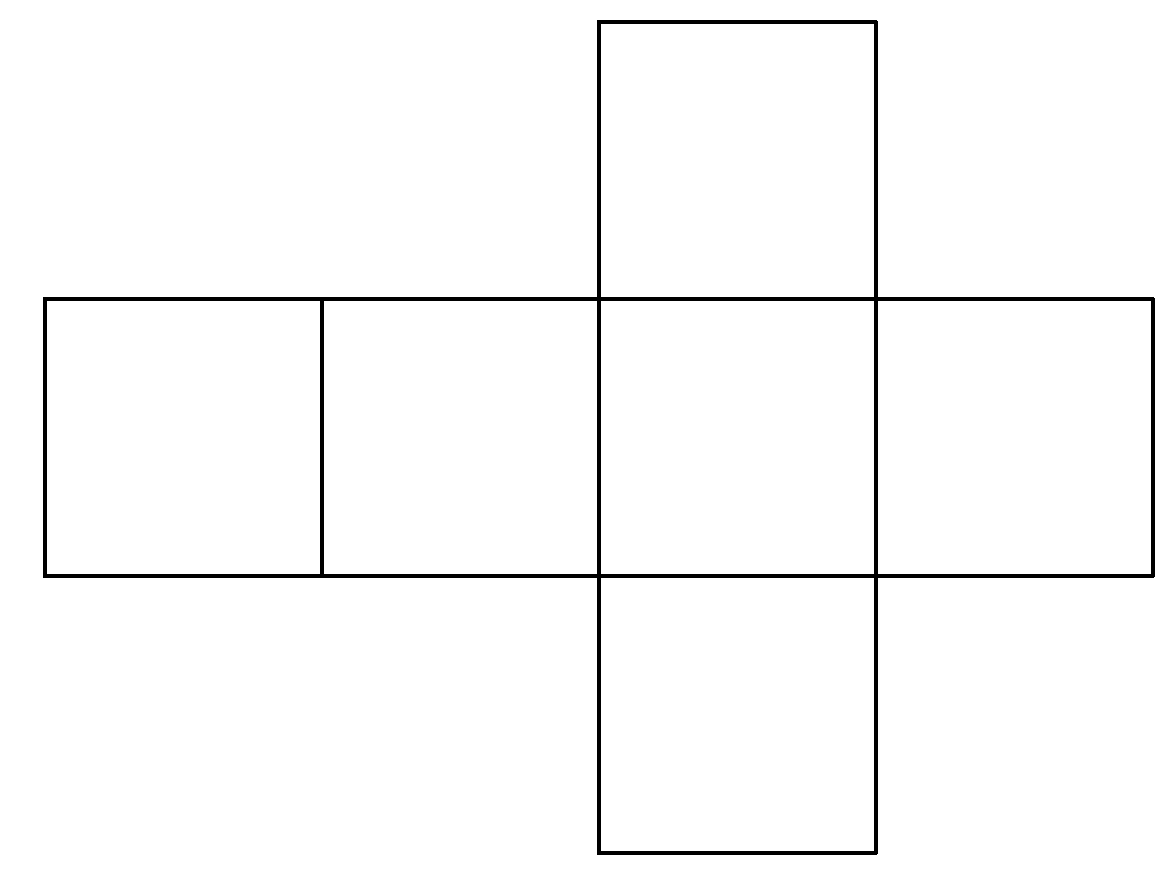
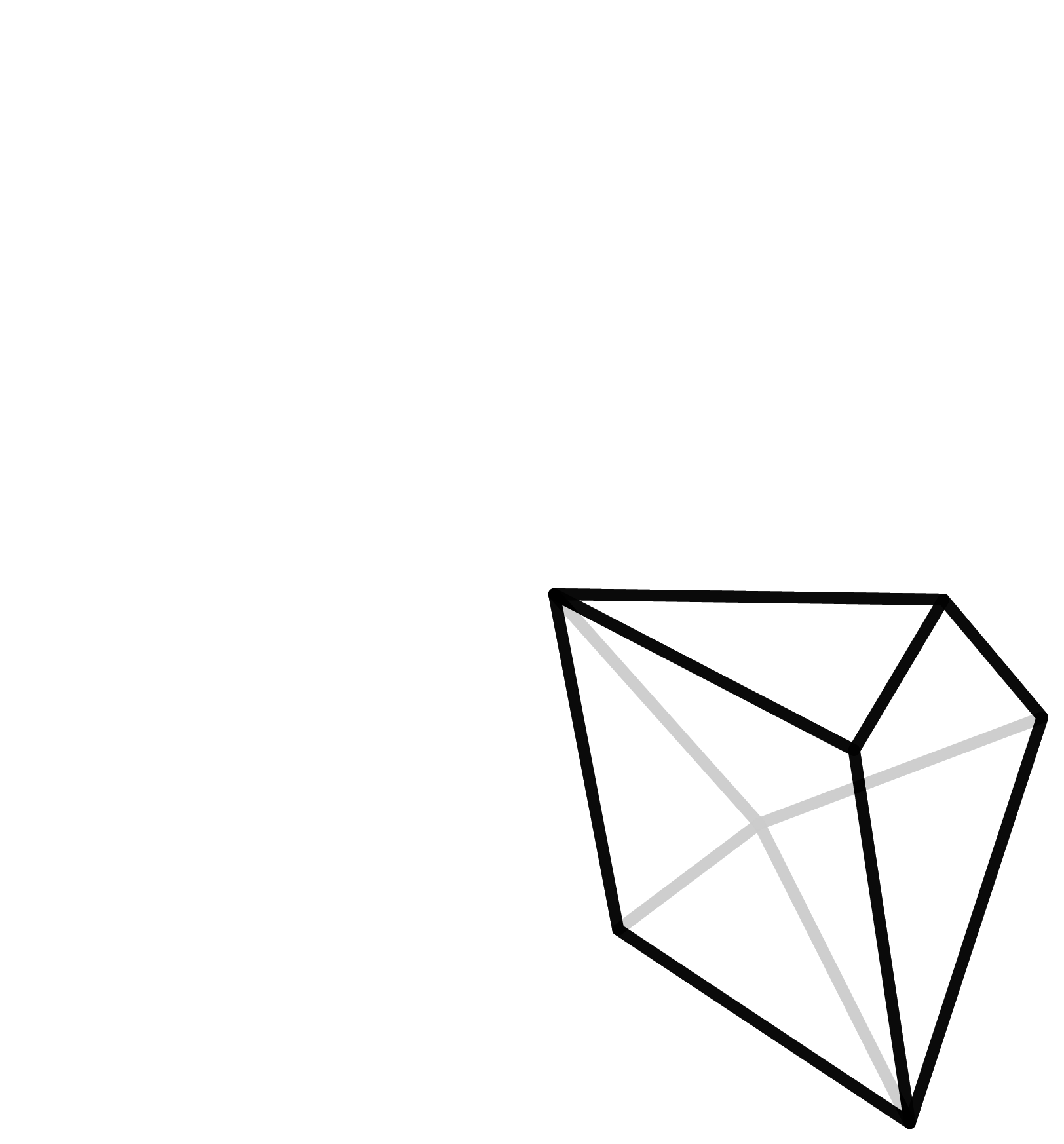
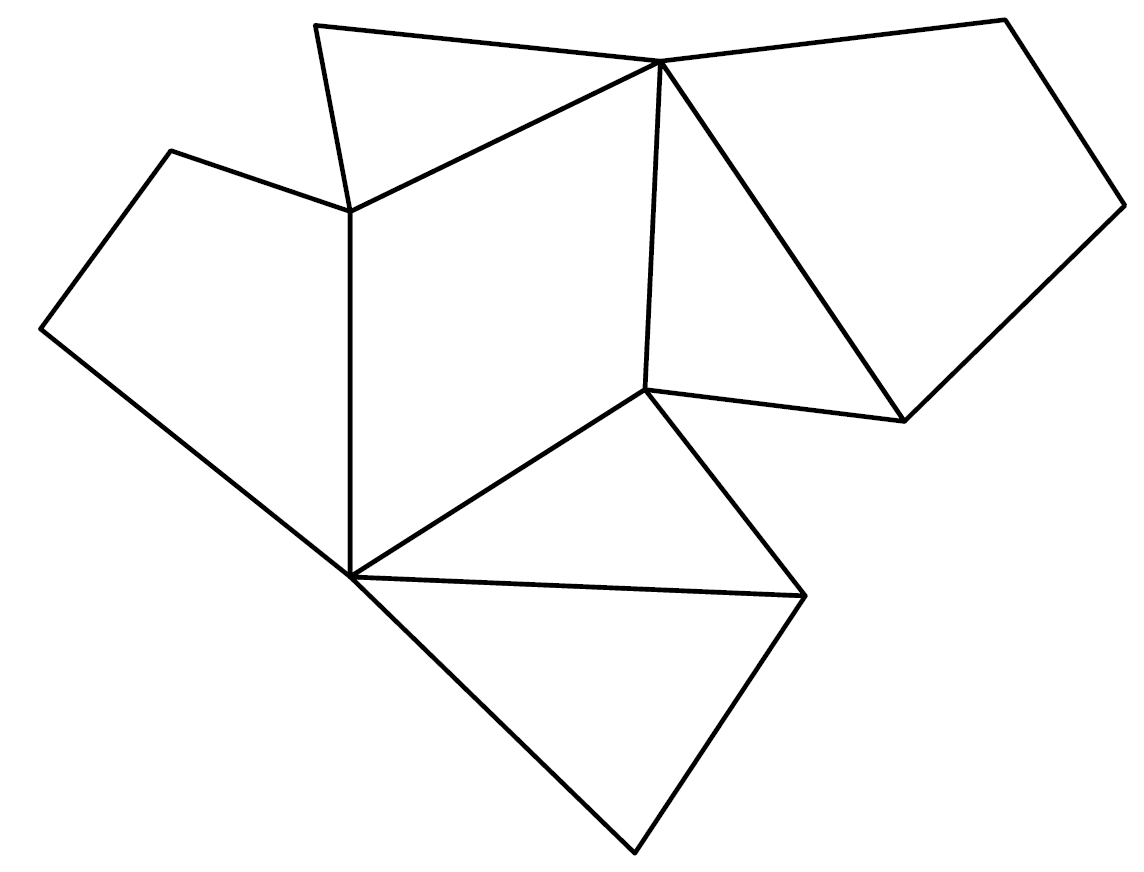
Ein Würfel mit seinem Netz sowie ein Polyeder mit sieben Ecken und das dazugehörige Netz.
Archimedische Körper
Die archimedischen Körper bilden eine weitere Klasse von sehr symmetrischen und damit manchmal als schön bezeichneten Polyedern. Auch sie bestehen nur aus gleichseitigen Vielecken, aber, anders als bei den platonischen Körpern, nicht nur aus denselben. Der Fußball ist wohl der bekannteste archimedische Körper. Mathematikerinnen und Mathematiker nennen ihn auch Ikosaederstumpf, denn er entsteht, wenn man bei einem Ikosaeder an jeder Ecke die Spitze abschneidet.

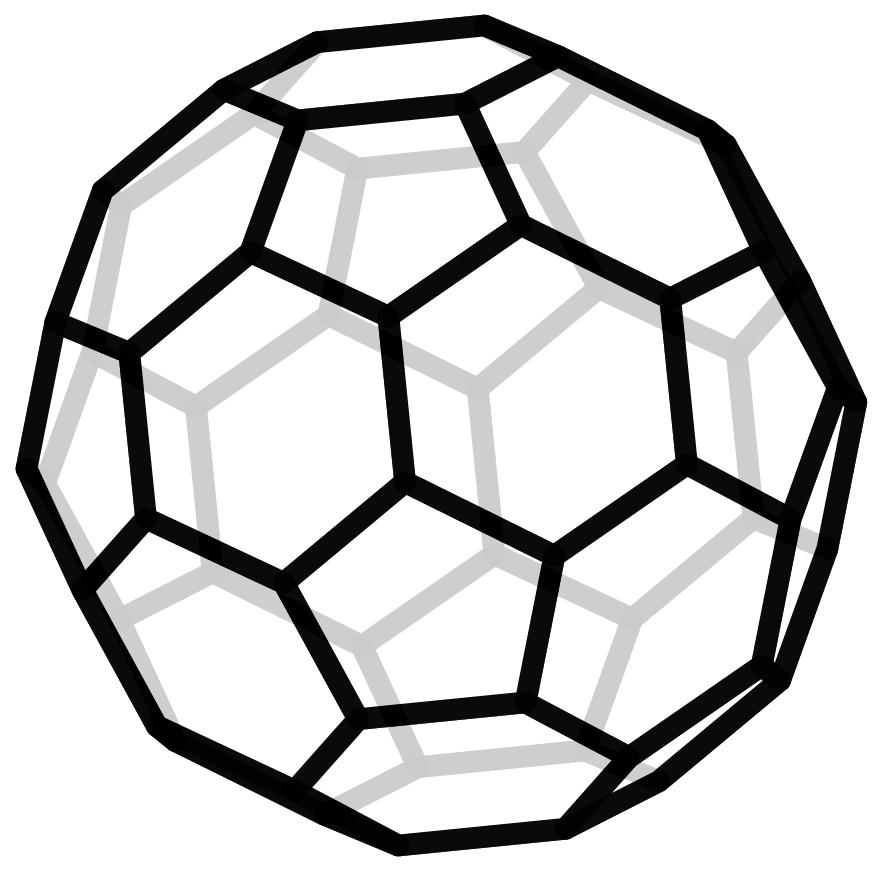
Links der Ikosaeder und rechts sein Ikosaederstumpf (oder Fußball).
Wie viele Polyeder gibt es?
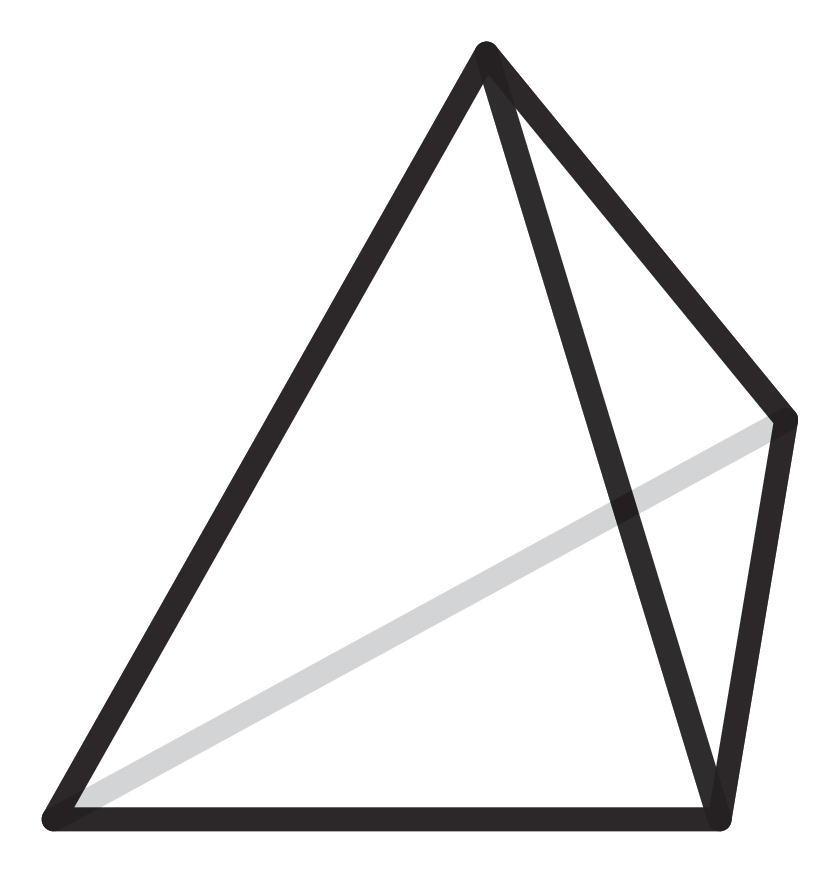
Für jede feste Anzahl an Ecken gibt es eine bestimmte Anzahl an Polyedern. In der Tabelle ist die Anzahl der Ecken der Anzahl der verschiedenen Typen von Polyedern zugeordnet. Man erkennt, dass die Anzahl der Typen rapide ansteigt. So gibt es nur ein einziges Polyeder mit vier Ecken: das Tetraeder. Verteilt man nämlich vier Punkte im Raum, so liegen sie entweder alle auf einer Ebene, oder man erhält immer eine Pyramide über einem Dreieck.
| Ecken | Polyeder |
| 4 | 1 |
| 5 | 2 |
| 6 | 7 |
| 7 | 34 |
| 8 | 257 |
| 9 | 2.606 |
| 10 | 32.300 |
| 11 | 440.564 |
| 12 | 6.384.634 |
| 13 | 96.262.938 |
| 14 | 1.496.225.352 |
| 15 | 23.833.988.129 |
| 16 | 387.591.510.244 |
| 17 | 6.415.851.530.241 |
| 18 | 107.854.282.197.058 |
| 19 | ??? |
Für fünf Ecken gibt es nur zwei Möglichkeiten: die Pyramide über einem Viereck, wenn vier der fünf Punkte auf einer Ebene liegen, oder die Doppelpyramide über einem Dreieck. Die sieben verschiedenen Typen von 6-eckigen Polyedern zu finden, wird dann schon langsam komplizierter.
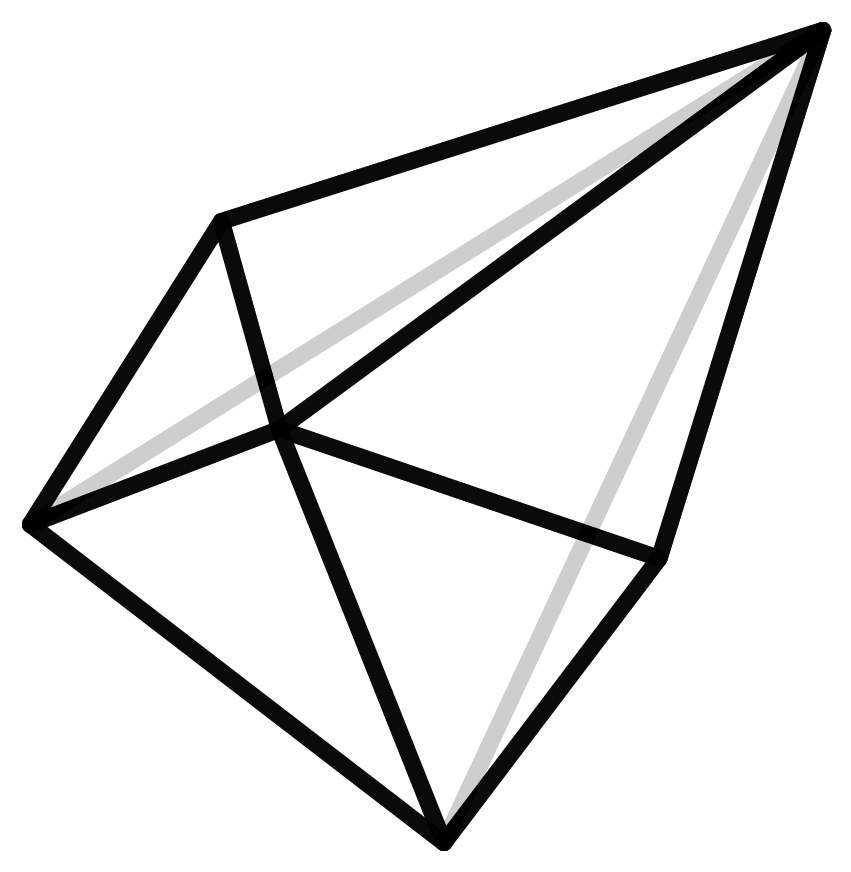
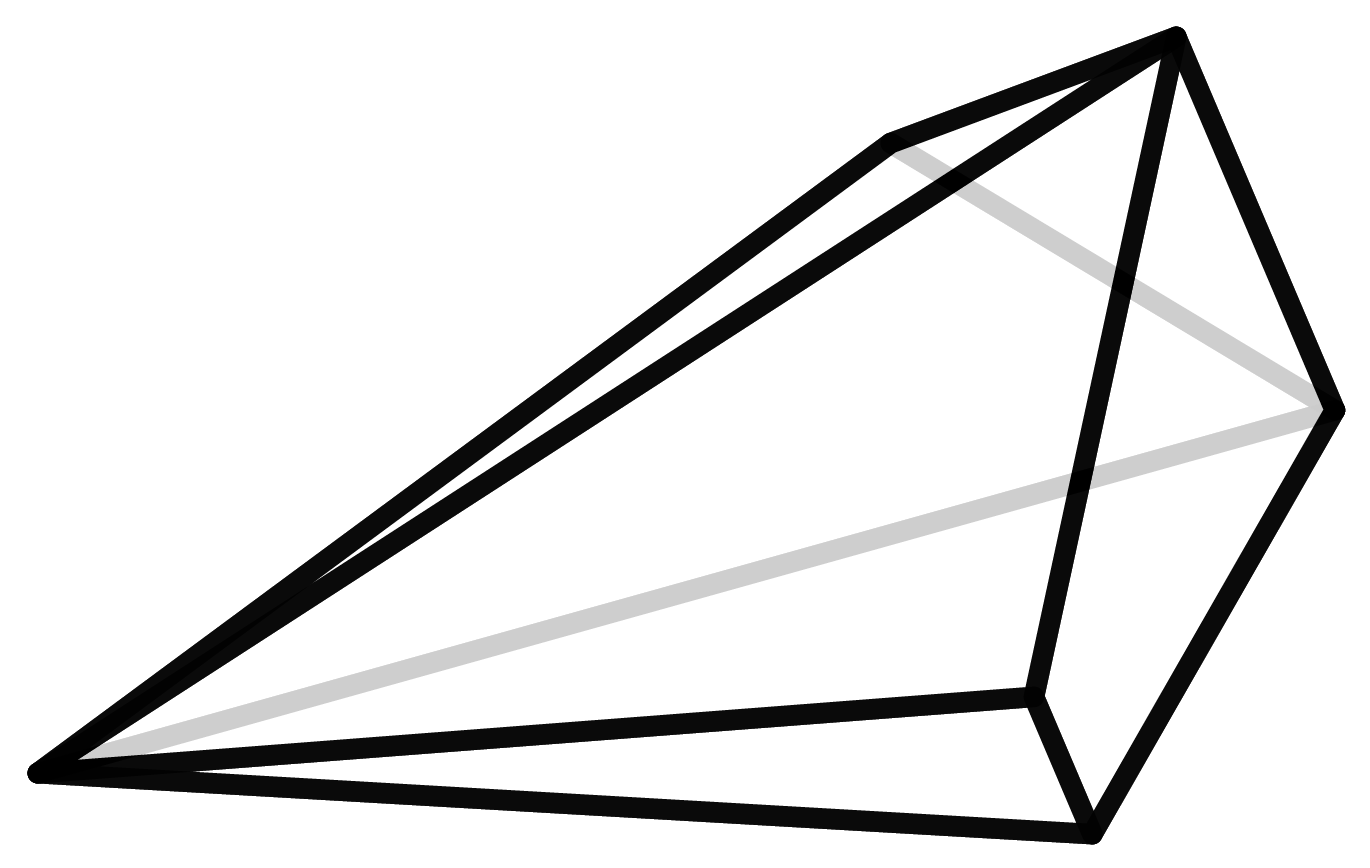
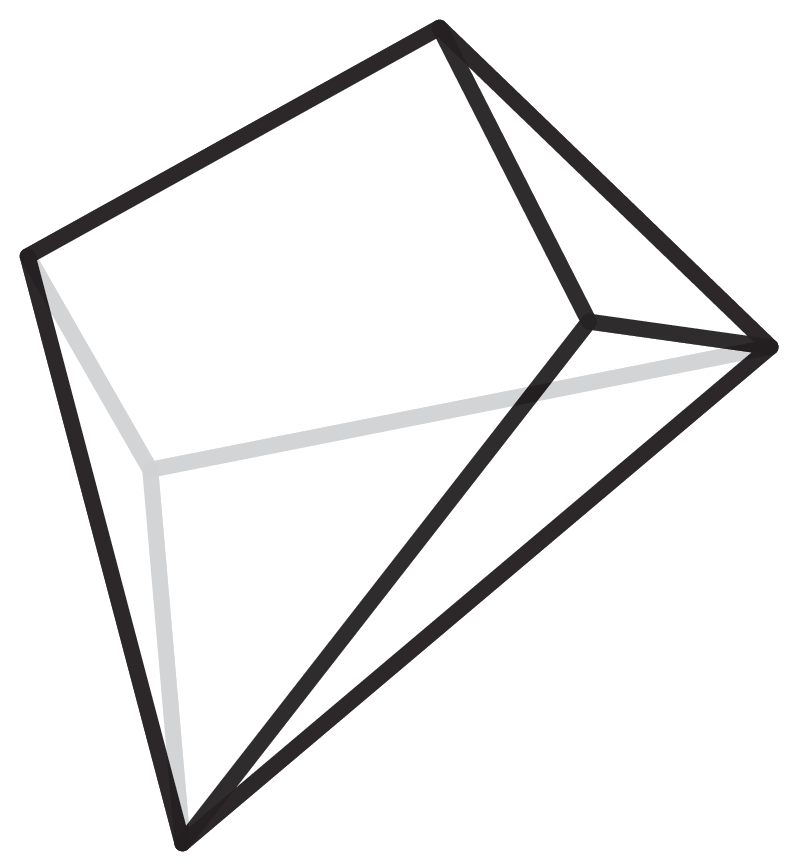
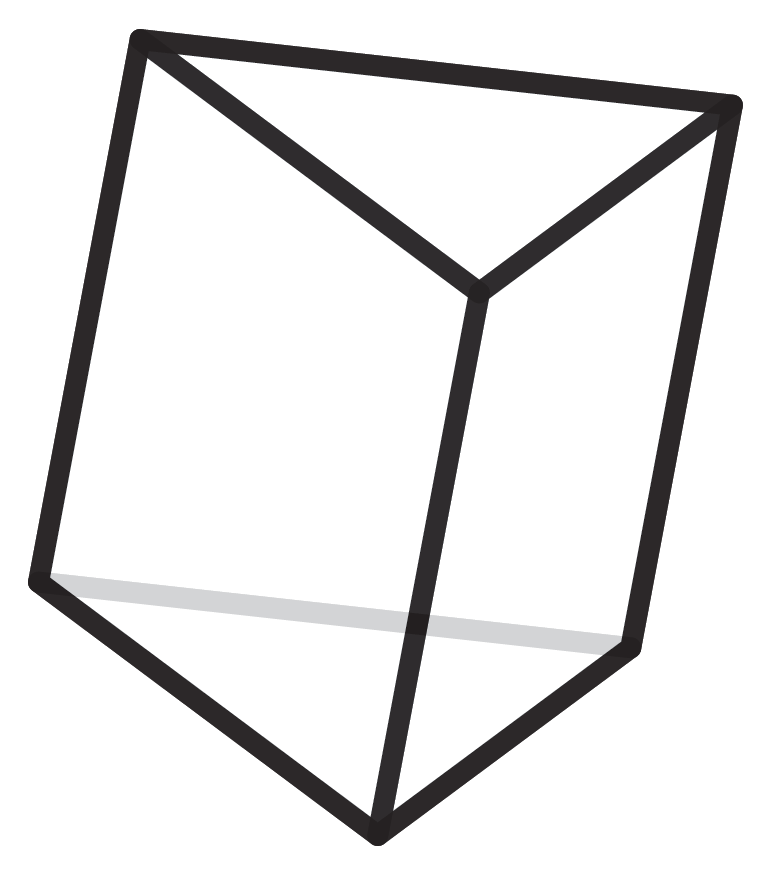
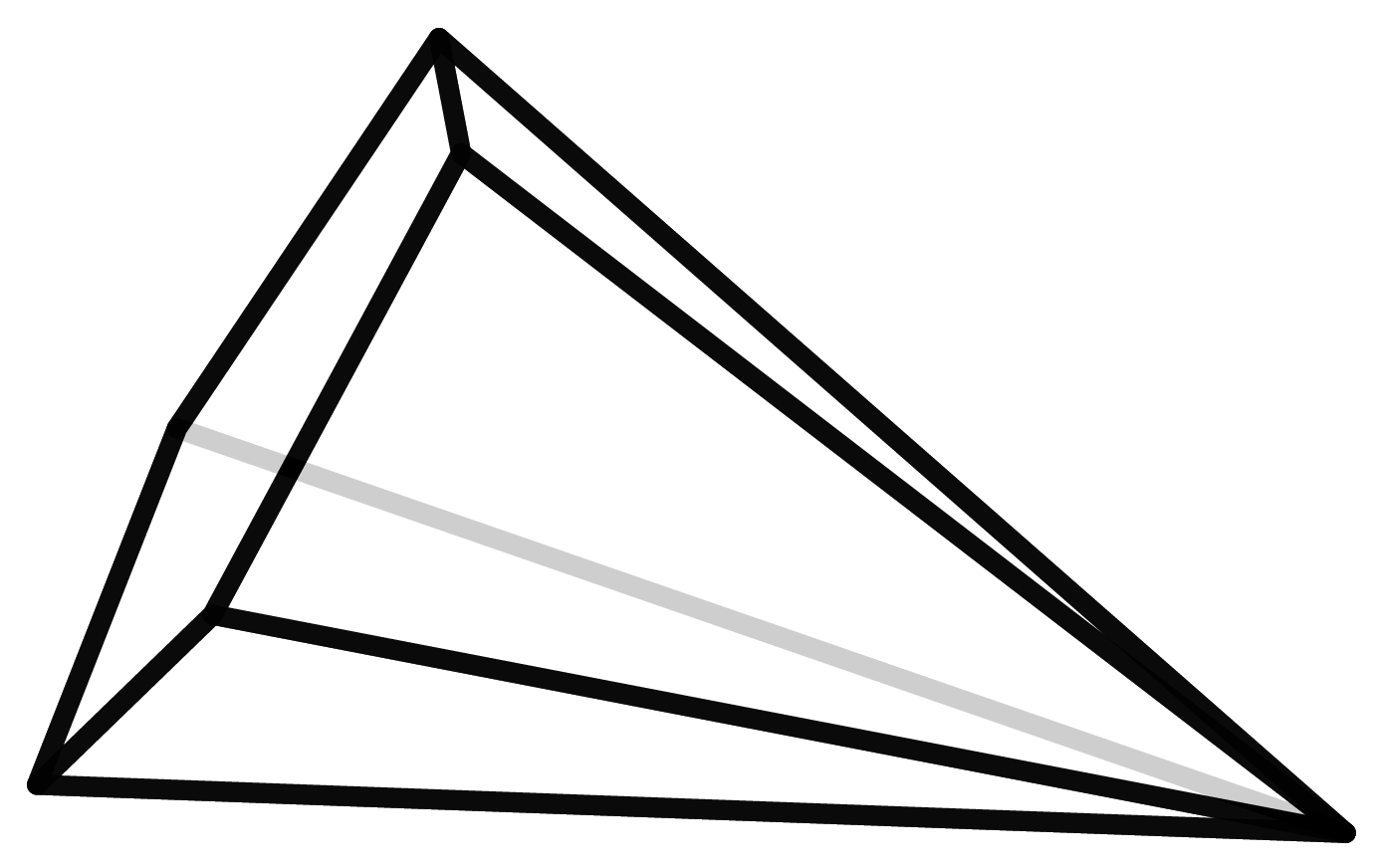
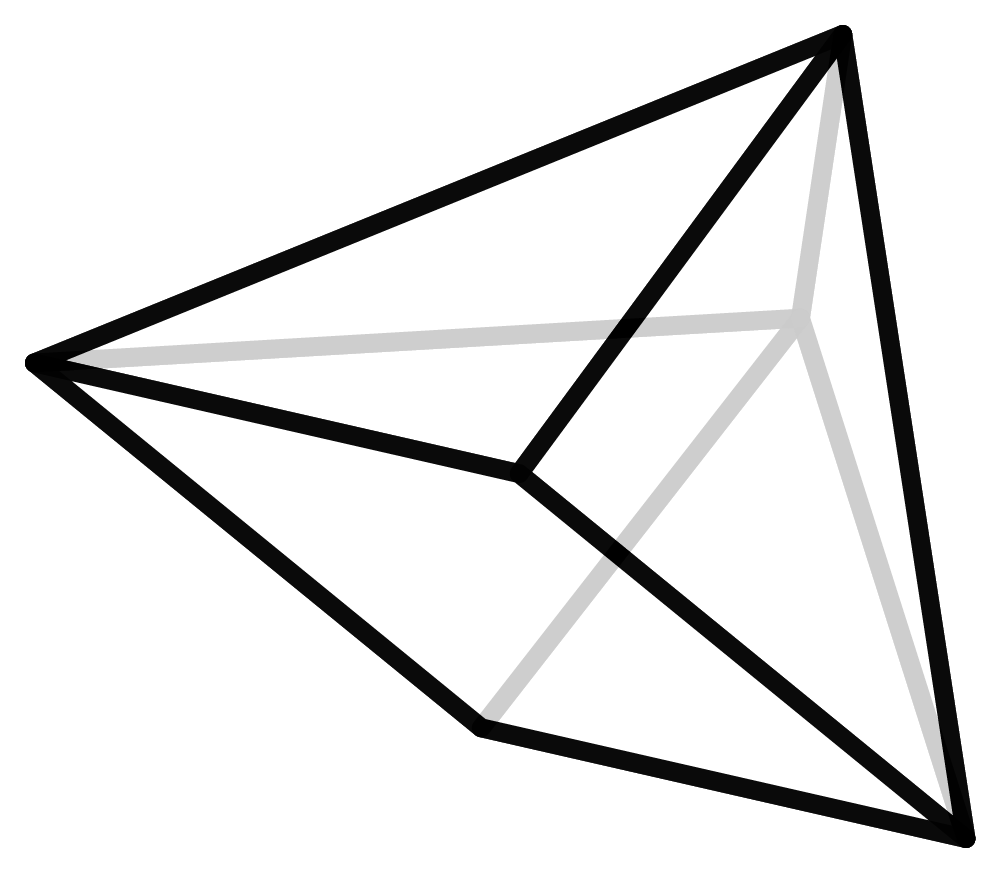

Um herauszufinden, wie viele Polyeder einer gewissen Anzahl es tatsächlich gibt, müssen wir sie auflisten. Dazu müssen alle erstellt werden. Woher aber weiß man, dass diese Liste vollständig ist und kein Polyeder doppelt vorkommt? In der Geometrie gibt es den Satz von Steinitz, der besagt, dass jedes Polyeder eindeutig einem Graphen mit einer bestimmten Eigenschaft zugeordnet werden kann. (Hier geht es um die Protagonisten aus der Graphentheorie und nicht diejenigen, die in Koordinatensystemen zu Hause sind.) Diese Graphen sind mathematisch leichter zu fassen und damit abzuzählen. Doch auch hierfür benötigt man einen Computer, da die Zahlen schnell sehr groß werden. Die Anzahl der sieben- und achteckigen Polyeder, nämlich 34 bzw. 257 Stück, wurden bereits im Jahre 1899 gefunden. Bis zur Entdeckung der 2606 neuneckigen Polyeder im Jahre 1969 war die Erfindung des Computers notwendig.
Dimensionen
In der Mathematik gibt es viele Möglichkeiten Dimensionen zu interpretieren. Der zugänglichste ist, sich die Dimensionen als Variablen vorzustellen. Einen Apfelkuchen zum Beispiel, der aus 6 Zutaten, sagen wir: Mehl, Butter, Zucker, Eiern, Backpulver und Äpfeln besteht, kann man als sechsdimensionales Objekt verstehen.
Durch das Betrachten von Fotos und Filmen, die ja immer eine Darstellung unserer dreidimensionalen Welt in einem zweidimensionalen Medium sind, sind wir es gewohnt eine Dimension mehr zu sehen. Den Vorgang des Abbildens einer höheren Dimension in eine niedrigere, also wenn man ein Foto, dass ja zweidimensional ist, von der dreidimensionalen Welt macht, nennt man in der Mathematik Projektion. Da es leider nicht möglich ist, den vierdimensionalen Raum im uns umgebenden dreidimensionalen Raum wirklich unterzubringen, müssen wir uns mit Projektionen behelfen.
Betrachtet man zum Beispiel den Würfel, so bestehen seine Seitenflächen aus Quadraten. Ein Quadrat kann man sich, da alle seine Kanten gleich lang sind, als einen zweidimensionalen Würfel vorstellen. Die Seiten des dreidimensionalen Würfels sind demnach zweidimensionale Würfel. Dieser Zusammenhang lässt sich auch auf höhere Dimensionen übertragen. Die Seitenflächen eines vierdimensionalen Würfels bestehen dann aus dreidimensionalen Würfeln. Es entsteht ein sogenannter Tesserakt. Hier ist ein Link zu einem Video (mit Untertiteln) in dem dieser Zusammenhang noch einmal graphisch visualisiert wird.
Konvex/Konvexität
Wenn wir von Polyedern sprechen, setzen wir stillschweigend voraus, dass es sich um konvexe Polyeder handelt. Konvex bedeutet, dass es keine Einbuchtungen nach innen, Aushöhlungen oder Löcher gibt. Die mathematisch korrekte Definition von Konvexität besagt, dass es für je zwei Punkte, die innerhalb einer Menge liegen auch ihre Verbindungsstrecke komplett innerhalb der Menge liegen muss.
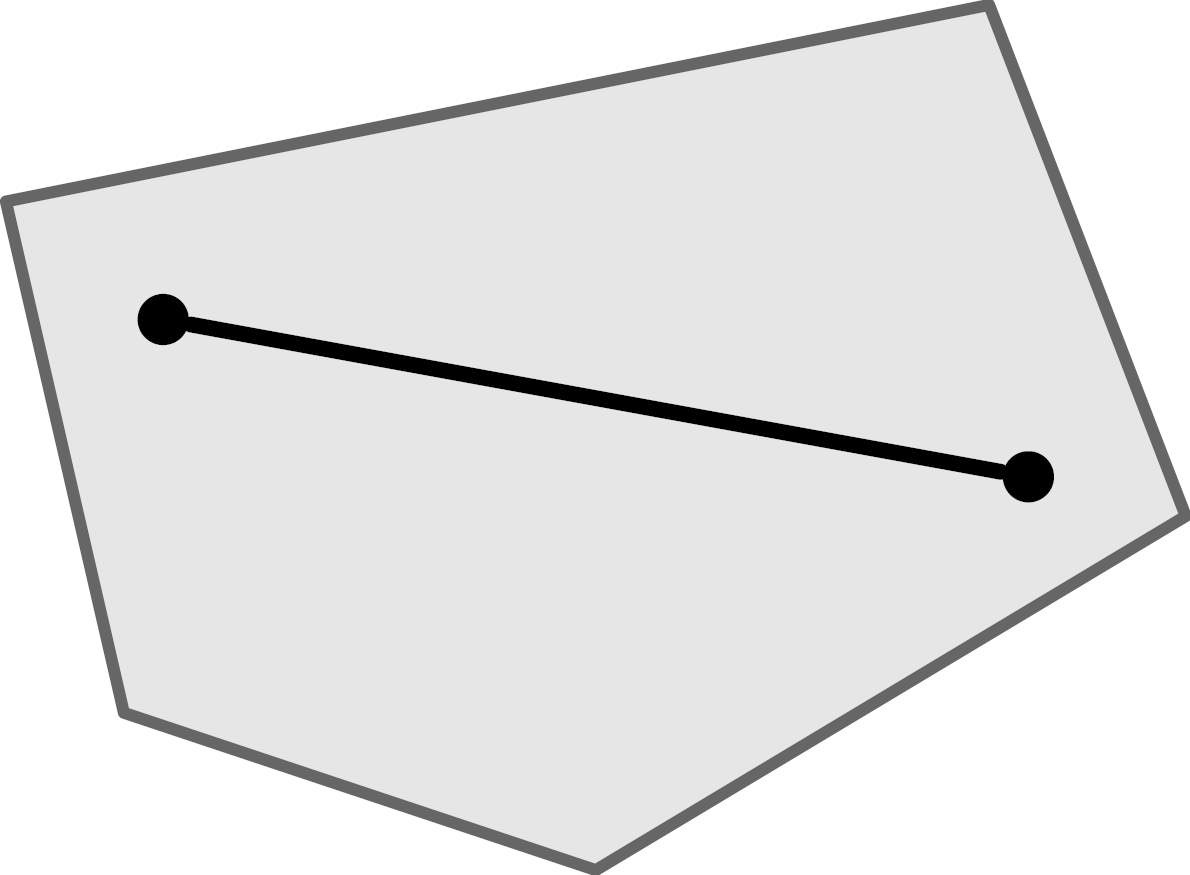
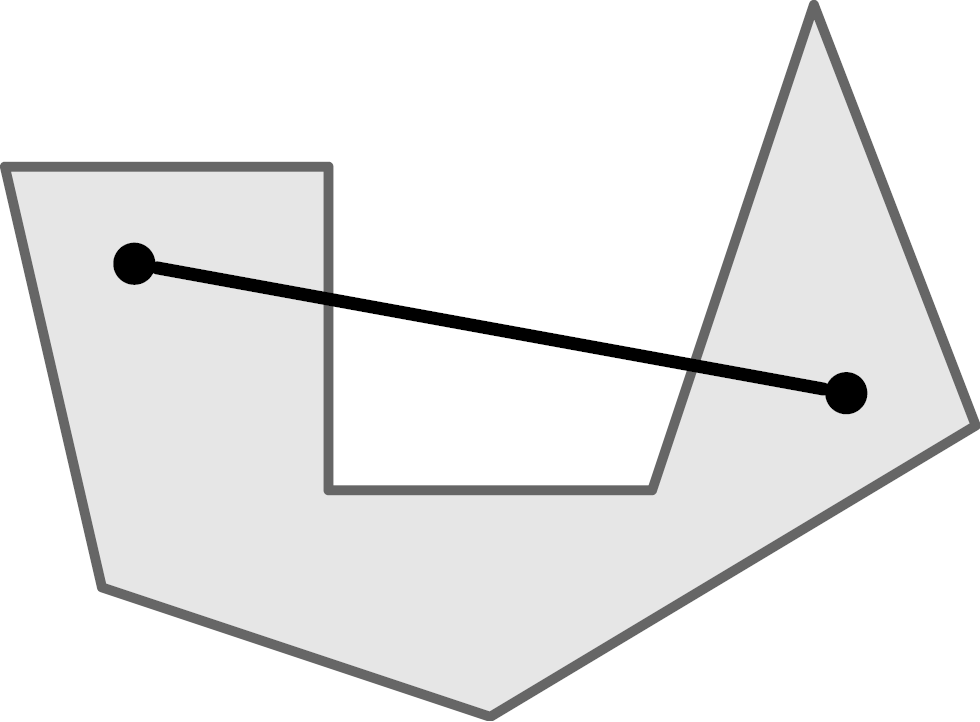
Links ein konvexes Objekt, rechts ein Objekt, das nicht konvex ist.
Kombinatorischer Typ
Jedes Polyeder kann auf verschiedene Arten geometrisch realisiert werden. Es kann groß oder klein sein, seine Form kann sich verändern, solange die Struktur der Ecken, Kanten und Flächen dieselbe bleibt. Diese Struktur, das Zusammentreffen der Kanten in den Ecken und die Anzahl der Ecken, die zu einer Fläche gehören, nennt man den kombinatorischen Typ eines Polyeders. Wir nennen zwei Polyeder kombinatorisch äquivalent, wenn sie denselben kombinatorischen Typ besitzen. d. h. wenn man die Ecken eindeutig einander zuordnen kann, so dass, wenn zwei Ecken in einem Polyeder durch eine Kante verbunden sind, auch die Ecken im anderen Polyeder eine gemeinsame Kante besitzen. Jedes Polyeder hat unendlich viele verschiedene geometrische Realisierungen. Wenn Du Dir hier auf Polytopia.eu ein Polyeder aussuchst, adoptierst du gleich den ganzen kombinatorischen Typ. Das bedeutet, dass du eigentlich gleich unendlich viele Polyeder adoptiert hast. Damit es aber nicht ganz so unübersichtlich ist, und du auch irgendwann mal mit dem Modellbauen fertig wirst, haben wir uns auf eine eindeutige Realisierung der Polyeder festgelegt. Es sind die sogenannten Koebe-Andreev-Thurston-Realisierungen der Polyeder. Ihre Besonderheit ist, dass im Inneren des Polyeders eine Kugel einbeschrieben ist, die jede der Kanten des Polyeders an genau einem Punkt berührt. Insbesondere beinhaltet jede Seitenfläche damit einen Kreis, der die Kanten genau einmal sanft berührt.

f-Vektor
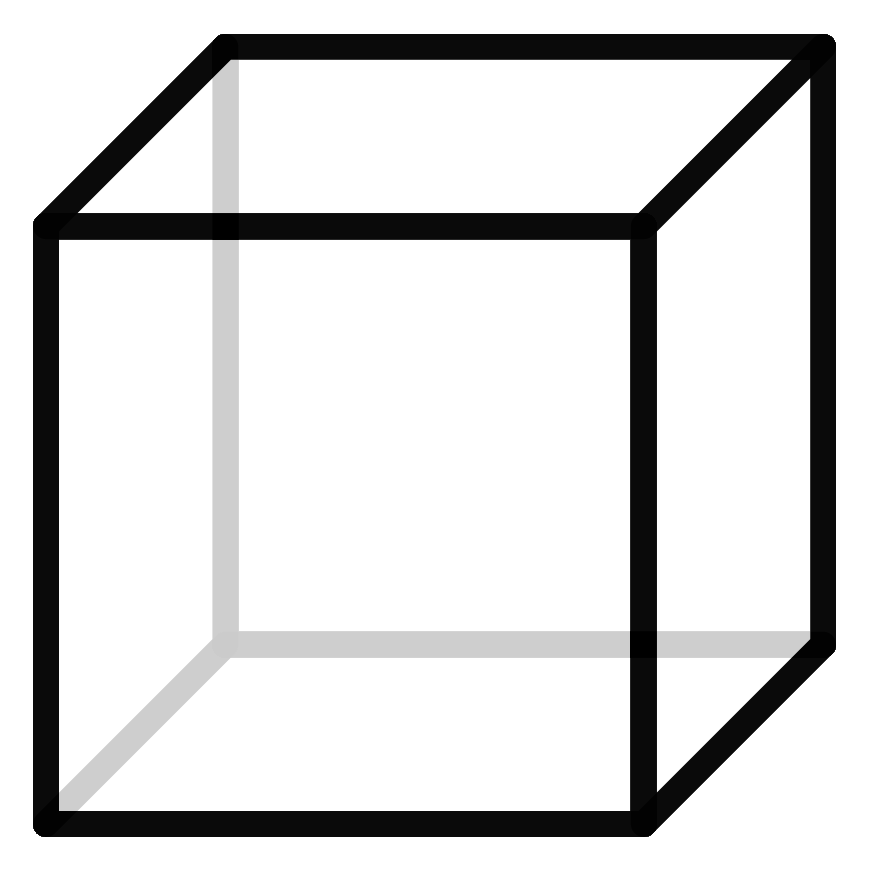
Der f-Vektor eines Polyeders gibt an, wie viele Ecken, Kanten und Seitenflächen es besitzt. Ein Vektor ist in diesem Fall keine geometrische Größe, sondern nur die Art und Weise der Darstellung dieser Zahlen. Der Würfel besteht aus 8 Ecken, 12 Kanten und 6 Seitenflächen und hat somit den f-Vektor (8,12,6). Durch diesen Vektor sind die Polyeder allerdings nicht eindeutig bestimmt. Es kann andere Polyeder mit demselben f-Vektor geben, die eine völlig andere Struktur haben. Diese Polyeder nennen wir auch Geschwister.

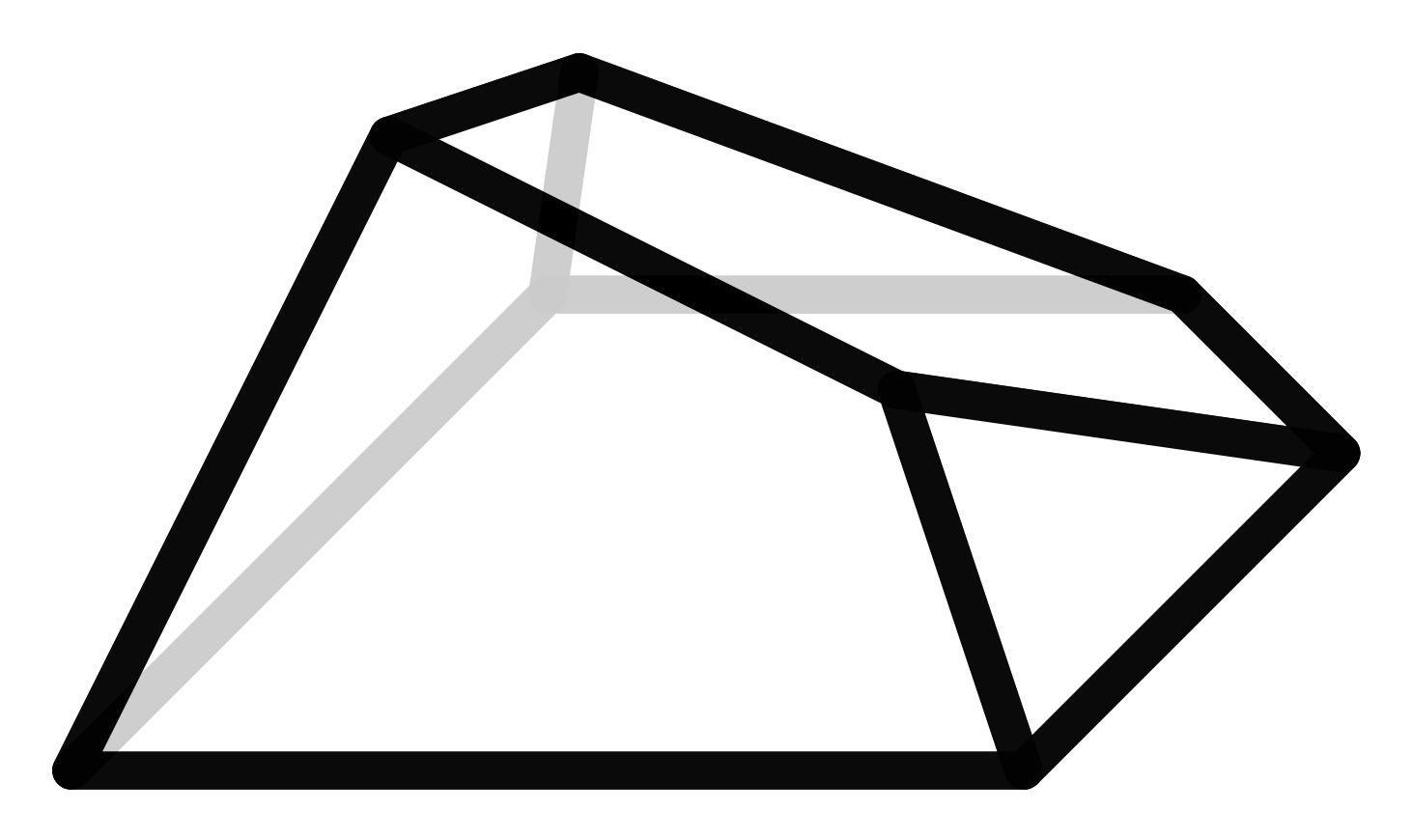
Hier sehen wir den Würfel und seine Schwester, die ebenfalls 6 Seitenflächen, 12 Kanten und 8 Ecken besitzt, jedoch eine ganz andere Struktur hat als der Würfel.
Mathematische Modelle
Mathematische Modelle und deren Bau spielten in der wissenschaftlichen Mathematik lange eine wichtige Rolle. Zum einen gab es einfach keine andere Möglichkeit, um sich zu einer Anschauung im Raum zu verhelfen. Natürlich kann man dreidimensionale Modelle auch zeichnen, dann erhält man aber immer nur eine Projektion des Raumes in die Ebene, wie bei einem Foto. Bei diesen macht uns das Erkennen des Raumes keine Probleme, weil wir ja wissen, dass ein Tisch meistens rechtwinklig ist. Sehen wir einen perspektivisch verzerrten Tisch auf einem Foto, so wissen wir intuitiv, dass er eigentlich rechtwinklig ist. Anders ist das natürlich, wenn man überhaupt erst mal begreifen möchte, welche Struktur ein geometrisches Objekt besitzt. Um z. B. eine Symmetrieachse zu erkennen, ist es sehr hilfreich einen Körper tatsächlich in der Hand halten und drehen zu können.
Modelle dienten jedoch nicht nur dem eigenen Erkenntnisgewinn, sondern auch der Wissensvermittlung. Um die eigene Forschung anderen zugänglich zu machen, brauchten Mathematikerinnen und Mathematiker eine Möglichkeit zur Visualisierung. Heutzutage wird dies vor allem mit dem Computer gemacht. Es gibt zahlreiche Möglichkeiten mathematische und geometrische Graphiken zu erzeugen. Durch Rotation eines Modells wird auch dem Problem der Einschränkung auf den flachen Bildschirm entgegengewirkt.
Dürers Vermutung
Obwohl sich schon seit der Antike Mathematikerinnen und Mathematiker mit Polyedern beschäftigen, ist noch lange nicht alles über sie bekannt. Ein „schönes“, weil leicht verständliches und doch bislang ungelöstes Problem ist die sogenannte Dürer’sche Vermutung. Der Maler Albrecht Dürer hat sich einige Jahre lang intensiv mit Mathematik beschäftigt. Auf ihn geht auch das Konzept des Polyedernetzes zurück. In seinem Buch „Underweysung der Messung, mit dem Zirckel und Richtscheyt“ zeichnete er Netze von verschiedenen Polyedern.
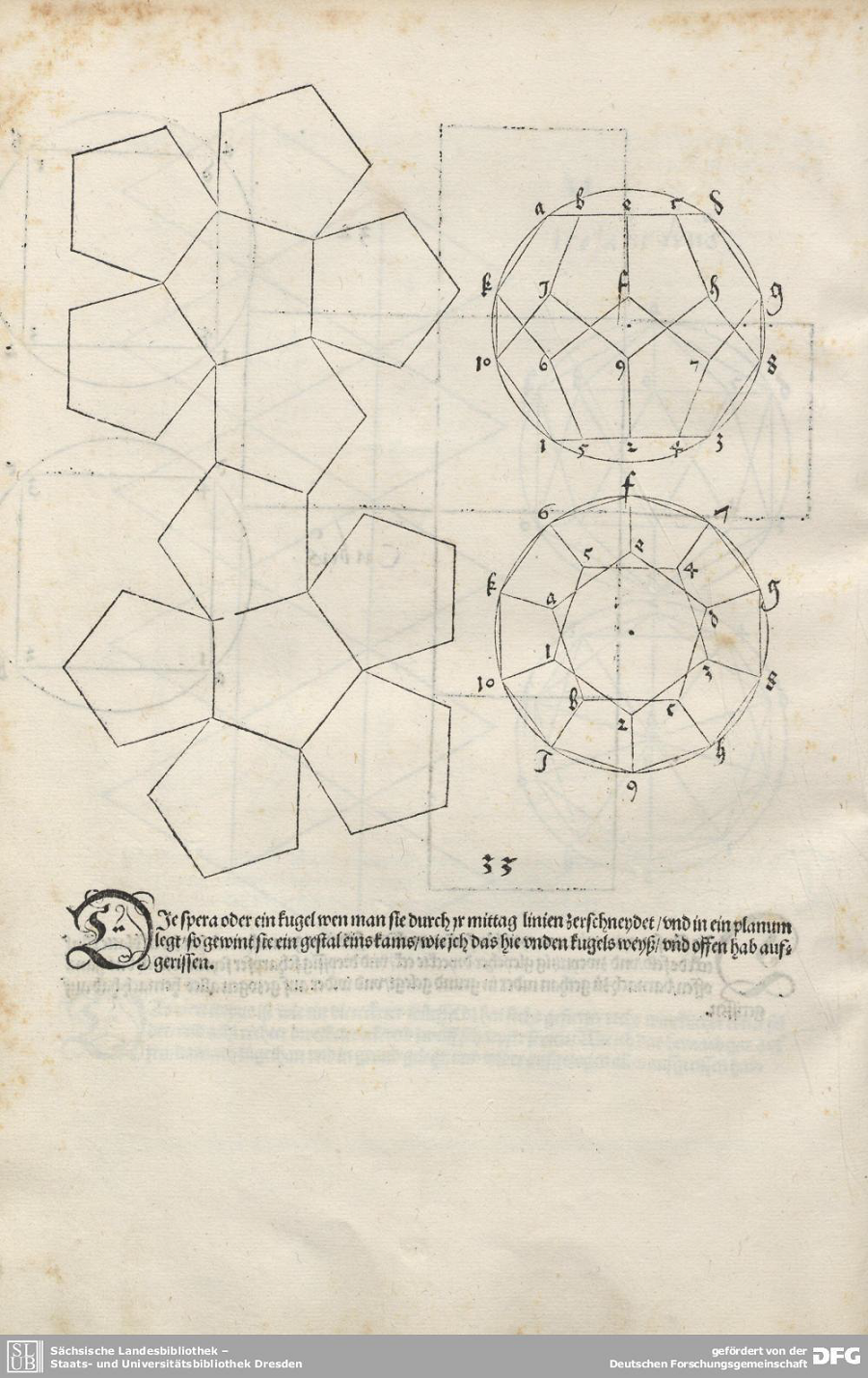
Ein Polyedernetz entsteht, indem man das Polyeder als leere Hülle betrachtet, die man nun entlang seiner Kanten so aufschneidet, dass sie zusammenhängend bleibt, aber flach aufgeklappt werden kann. Auf diese Weise entsteht eine Art Bastelbogen für das Polyeder. Die Frage hinter Dürers Vermutung lautet nun, ob dies mit jedem Polyeder so möglich ist, dass sich die Seitenflächen in der Ebene nicht überschneiden. Besitzt also jedes Polyeder einen Bastelbogen?
Bis heute haben sich viele Mathematikerinnen und Mathematiker mit diesem Problem beschäftigt. Es gibt erste Zwischenergebnisse. Zum Bespiel ist bekannt, dass man jedes beliebige Polyeder so in die Länge ziehen kann, dass es dann überschneidungsfrei aufgeklappt werden kann (s. https://arxiv.org/pdf/1305.3231.pdf). Dadurch ändert sich zwar die geometrische Realisierung des Polyeders, nicht aber seine Struktur. Auf der anderen Seite ist das Tetraeder das einzige Polyeder, für das wir wirklich wissen, dass es immer aufgeklappt werden kann, egal wie sehr es verzerrt ist.
Da wir die Polyedernetze und somit die Bastelbögen der Polyeder automatisch generiert haben, ist es möglich, dass das Netz deines adoptierten Polyeders sich überschneidet und somit nicht ausgeschnitten werden kann. Sollte das bei deinem Polyeder so sein: Schreib uns eine E-Mail!
Geschwister
Wir nennen Polyeder Geschwister, wenn sie dieselbe Anzahl von Ecken, Kanten und Seitenflächen, also denselben f-Vektor, haben. Wie menschliche Geschwister sehen sich manche sehr ähnlich, andere wiederum haben eine völlig andere Form. Der Würfel besteht aus 8 Ecken, 12 Kanten und 6 Seitenflächen. Diese Zahlen definieren ihn also nicht eindeutig, denn es gibt auch andere Polyeder mit diesem f-Vektor, die eine völlig andere Struktur haben.
Geschwister:Poliedro filosofal , Cookie123, Polytorsten, Armetisti, Backflip, Renes PolyWas?, Pollister , Polimili, Rain, Pol el politopo, Gautamahedron, PengPeng, Geschwisterchen 1000009, Geschwisterchen 1000014, Geschwisterchen 1000017, Geschwisterchen 1000019, Geschwisterchen 1000023, Geschwisterchen 1000025, Geschwisterchen 1000029, Geschwisterchen 1000031, . . .
Geschwisterchen 1000040, Geschwisterchen 1000042, Geschwisterchen 1000044, Geschwisterchen 1000045, Geschwisterchen 1000049, Geschwisterchen 1000078, Geschwisterchen 1000085, Geschwisterchen 1000090, Geschwisterchen 1000093, Geschwisterchen 1000116, Geschwisterchen 1000119, Geschwisterchen 1000123, Geschwisterchen 1000126, Geschwisterchen 1000129, Geschwisterchen 1000134, Geschwisterchen 1000136, Geschwisterchen 1000140, Geschwisterchen 1000142, Geschwisterchen 1000152, Geschwisterchen 1000157, Geschwisterchen 1000159, Geschwisterchen 1000161, Geschwisterchen 1000165, Geschwisterchen 1000169, Geschwisterchen 1000171, Geschwisterchen 1000174, Geschwisterchen 1000176, Geschwisterchen 1000179, Geschwisterchen 1000180, Geschwisterchen 1000182, Geschwisterchen 1000184, Geschwisterchen 1000189, Geschwisterchen 1000190, Geschwisterchen 1000194, Geschwisterchen 1000199, Geschwisterchen 1000200, Geschwisterchen 1000201, Geschwisterchen 1000204, Geschwisterchen 1000205, Geschwisterchen 1000216, Geschwisterchen 1000218, Geschwisterchen 1000220, Geschwisterchen 1000225, Geschwisterchen 1000226, Geschwisterchen 1000229, Geschwisterchen 1000231, Geschwisterchen 1000234, Geschwisterchen 1000248, Geschwisterchen 1000262, Geschwisterchen 1000263, Geschwisterchen 1000265, Geschwisterchen 1000268, Geschwisterchen 1000281, Geschwisterchen 1000300, Geschwisterchen 1000301, Geschwisterchen 1000304, Geschwisterchen 1000308, Geschwisterchen 1000309, Geschwisterchen 1000312, Geschwisterchen 1000316, Geschwisterchen 1000324, Geschwisterchen 1000331, Geschwisterchen 1000343, Geschwisterchen 1000346, Geschwisterchen 1000348, Geschwisterchen 1000356, Geschwisterchen 1000357, Geschwisterchen 1000389, Geschwisterchen 1000405, Geschwisterchen 1000409, Geschwisterchen 1000414, Geschwisterchen 1000418, Geschwisterchen 1000425, Geschwisterchen 1000427, Geschwisterchen 1000451, Geschwisterchen 1000453, Geschwisterchen 1000458, Geschwisterchen 1000460, Geschwisterchen 1000463, Geschwisterchen 1000467, Geschwisterchen 1000473, Geschwisterchen 1000480, Geschwisterchen 1000481, Geschwisterchen 1000484, Geschwisterchen 1000487, Geschwisterchen 1000490, Geschwisterchen 1000492, Geschwisterchen 1000495, Geschwisterchen 1000496, Geschwisterchen 1000499, Geschwisterchen 1000514, Geschwisterchen 1000516, Geschwisterchen 1000517, Geschwisterchen 1000521, Geschwisterchen 1000523, Geschwisterchen 1000524, Geschwisterchen 1000527, Geschwisterchen 1000531, Geschwisterchen 1000534, Geschwisterchen 1000537, Geschwisterchen 1000541, Geschwisterchen 1000543, Geschwisterchen 1000547, Geschwisterchen 1000549, Geschwisterchen 1000551, Geschwisterchen 1000553, Geschwisterchen 1000557, Geschwisterchen 1000559, Geschwisterchen 1000561, Geschwisterchen 1000562, Geschwisterchen 1000567, Geschwisterchen 1000569, Geschwisterchen 1000571, Geschwisterchen 1000576, Geschwisterchen 1000582, Geschwisterchen 1000584, Geschwisterchen 1000588, Geschwisterchen 1000590, Geschwisterchen 1000598, Geschwisterchen 1000602, Geschwisterchen 1000604, Geschwisterchen 1000605, Geschwisterchen 1000611, Geschwisterchen 1000612, Geschwisterchen 1000615, Geschwisterchen 1000619, Geschwisterchen 1000622, Geschwisterchen 1000641, Geschwisterchen 1000644, Geschwisterchen 1000650, Geschwisterchen 1000652, Geschwisterchen 1000662, Geschwisterchen 1000669, Geschwisterchen 1000695, Geschwisterchen 1000706, Geschwisterchen 1000715, Geschwisterchen 1000716, Geschwisterchen 1000718, Geschwisterchen 1000723, Geschwisterchen 1000724, Geschwisterchen 1000725, Geschwisterchen 1000730, Geschwisterchen 1000732, Geschwisterchen 1000736, Geschwisterchen 1000740, Geschwisterchen 1000742, Geschwisterchen 1000761, Geschwisterchen 1000768, Geschwisterchen 1000770, Geschwisterchen 1000779, Geschwisterchen 1000780, Geschwisterchen 1000784, Geschwisterchen 1000809, Geschwisterchen 1000824, Geschwisterchen 1000826, Geschwisterchen 1000828, Geschwisterchen 1000830, Geschwisterchen 1000831, Geschwisterchen 1000835, Geschwisterchen 1000836, Geschwisterchen 1000840, Geschwisterchen 1000843, Geschwisterchen 1000846, Geschwisterchen 1000847, Geschwisterchen 1000849, Geschwisterchen 1000852, Geschwisterchen 1000856, Geschwisterchen 1000857, Geschwisterchen 1000858, Geschwisterchen 1000862, Geschwisterchen 1000864, Geschwisterchen 1000865, Geschwisterchen 1000869, Geschwisterchen 1000870, Geschwisterchen 1000872, Geschwisterchen 1000877, Geschwisterchen 1000880, Geschwisterchen 1000884, Geschwisterchen 1000886, Geschwisterchen 1000891, Geschwisterchen 1000892, Geschwisterchen 1000895, Geschwisterchen 1000897, Geschwisterchen 1000900, Geschwisterchen 1000906, Geschwisterchen 1000909, Geschwisterchen 1000916, Geschwisterchen 1000921, Geschwisterchen 1000924, Geschwisterchen 1000940, Geschwisterchen 1000946, Geschwisterchen 1000953, Geschwisterchen 1000955, Geschwisterchen 1000956, Geschwisterchen 1000993, Geschwisterchen 1001006, Geschwisterchen 1001009, Geschwisterchen 1001010, Geschwisterchen 1001013, Geschwisterchen 1001016, Geschwisterchen 1001019, Geschwisterchen 1001020, Geschwisterchen 1001036, Geschwisterchen 1001042, Geschwisterchen 1001048, Geschwisterchen 1001051, Geschwisterchen 1001056, Geschwisterchen 1001063, Geschwisterchen 1001066, Geschwisterchen 1001070, Geschwisterchen 1001073, Geschwisterchen 1001091, Geschwisterchen 1001093, Geschwisterchen 1001108, Geschwisterchen 1001109, Geschwisterchen 1001113, Geschwisterchen 1001114, Geschwisterchen 1001116, Geschwisterchen 1001120, Geschwisterchen 1001123, Geschwisterchen 1001127, Geschwisterchen 1001128, Geschwisterchen 1001140, Geschwisterchen 1001142, Geschwisterchen 1001147, Geschwisterchen 1001148, Geschwisterchen 1001151, Geschwisterchen 1001155, Geschwisterchen 1001157, Geschwisterchen 1001159, Geschwisterchen 1001161, Geschwisterchen 1001165, Geschwisterchen 1001167, Geschwisterchen 1001169, Geschwisterchen 1001172, Geschwisterchen 1001176, Geschwisterchen 1001178, Geschwisterchen 1001188, Geschwisterchen 1001192, Geschwisterchen 1001205, Geschwisterchen 1001207, Geschwisterchen 1001208, Geschwisterchen 1001209, Geschwisterchen 1001211, Geschwisterchen 1001219, Geschwisterchen 1001221, Geschwisterchen 1001223, Geschwisterchen 1001231, Geschwisterchen 1001241, Geschwisterchen 1001253, Geschwisterchen 1001257, Geschwisterchen 1001295, Geschwisterchen 1001304, Geschwisterchen 1001317, Geschwisterchen 1001325, Geschwisterchen 1001333, Geschwisterchen 1001335, Geschwisterchen 1001337, Geschwisterchen 1001339, Geschwisterchen 1001343, Geschwisterchen 1001347, Geschwisterchen 1001349, Geschwisterchen 1001354, Geschwisterchen 1001356, Geschwisterchen 1001361, Geschwisterchen 1001366, Geschwisterchen 1001367, Geschwisterchen 1001370, Geschwisterchen 1001375, Geschwisterchen 1001378, Geschwisterchen 1001379, Geschwisterchen 1001382, Geschwisterchen 1001387, Geschwisterchen 1001388, Geschwisterchen 1001390, Geschwisterchen 1001395, Geschwisterchen 1001398, Geschwisterchen 1001400, Geschwisterchen 1001403, Geschwisterchen 1001409, Geschwisterchen 1001412, Geschwisterchen 1001433, Geschwisterchen 1001439, Geschwisterchen 1001441, Geschwisterchen 1001447, Geschwisterchen 1001449, Geschwisterchen 1001452, Geschwisterchen 1001456, Geschwisterchen 1001458, Geschwisterchen 1001460, Geschwisterchen 1001461, Geschwisterchen 1001462, Geschwisterchen 1001469, Geschwisterchen 1001472, Geschwisterchen 1001474, Geschwisterchen 1001477, Geschwisterchen 1001478, Geschwisterchen 1001481, Geschwisterchen 1001484, Geschwisterchen 1001488, Geschwisterchen 1001489, Geschwisterchen 1001491, Geschwisterchen 1001494, Geschwisterchen 1001496, Geschwisterchen 1001499, Geschwisterchen 1001503, Geschwisterchen 1001506, Geschwisterchen 1001509, Geschwisterchen 1001510, Geschwisterchen 1001527, Geschwisterchen 1001530, Geschwisterchen 1001533, Geschwisterchen 1001561, Geschwisterchen 1001565, Geschwisterchen 1001569, Geschwisterchen 1001571, Geschwisterchen 1001572, Geschwisterchen 1001575, Geschwisterchen 1001579, Geschwisterchen 1001581, Geschwisterchen 1001582, Geschwisterchen 1001586, Geschwisterchen 1001589, Geschwisterchen 1001590, Geschwisterchen 1001593, Geschwisterchen 1001597, Geschwisterchen 1001606, Geschwisterchen 1001610, Geschwisterchen 1001612, Geschwisterchen 1001624, Geschwisterchen 1001649, Geschwisterchen 1001651, Geschwisterchen 1001656, Geschwisterchen 1001660, Geschwisterchen 1001670, Geschwisterchen 1001681, Geschwisterchen 1001714, Geschwisterchen 1001721, Geschwisterchen 1001724, Geschwisterchen 1001727, Geschwisterchen 1001730, Geschwisterchen 1001731, Geschwisterchen 1001736, Geschwisterchen 1001744, Geschwisterchen 1001747, Geschwisterchen 1001748, Geschwisterchen 1001750, Geschwisterchen 1001752, Geschwisterchen 1001755, Geschwisterchen 1001762, Geschwisterchen 1001765, Geschwisterchen 1001767, Geschwisterchen 1001773, Geschwisterchen 1001776, Geschwisterchen 1001778, Geschwisterchen 1001781, Geschwisterchen 1001783, Geschwisterchen 1001784, Geschwisterchen 1001786, Geschwisterchen 1001788, Geschwisterchen 1001792, Geschwisterchen 1001794, Geschwisterchen 1001802, Geschwisterchen 1001805, Geschwisterchen 1001806, Geschwisterchen 1001811, Geschwisterchen 1001813, Geschwisterchen 1001817, Geschwisterchen 1001820, Geschwisterchen 1001823, Geschwisterchen 1001824, Geschwisterchen 1001829, Geschwisterchen 1001830, Geschwisterchen 1001835, Geschwisterchen 1001837, Geschwisterchen 1001841, Geschwisterchen 1001846, Geschwisterchen 1001848, Geschwisterchen 1001850, Geschwisterchen 1001856, Geschwisterchen 1001857, Geschwisterchen 1001859, Geschwisterchen 1001873, Geschwisterchen 1001875, Geschwisterchen 1001877, Geschwisterchen 1001880, Geschwisterchen 1001882, Geschwisterchen 1001884, Geschwisterchen 1001886, Geschwisterchen 1001895, Geschwisterchen 1001897, Geschwisterchen 1001898, Geschwisterchen 1001900, Geschwisterchen 1001905, Geschwisterchen 1001907, Geschwisterchen 1001912, Geschwisterchen 1001914, Geschwisterchen 1001916, Geschwisterchen 1001919, Geschwisterchen 1001921, Geschwisterchen 1001925, Geschwisterchen 1001928, Geschwisterchen 1001939, Geschwisterchen 1001952, Geschwisterchen 1001963, Geschwisterchen 1001981, Geschwisterchen 1001983, Geschwisterchen 1001985, Geschwisterchen 1001991, Geschwisterchen 1001995, Geschwisterchen 1001997, Geschwisterchen 1002000, Geschwisterchen 1002035, Geschwisterchen 1002039, Geschwisterchen 1002057, Geschwisterchen 1002067, Geschwisterchen 1002069, Geschwisterchen 1002071, Geschwisterchen 1002072, Geschwisterchen 1002074, Geschwisterchen 1002078, Geschwisterchen 1002082, Geschwisterchen 1002083, Geschwisterchen 1002103, Geschwisterchen 1002109, Geschwisterchen 1002111, Geschwisterchen 1002115, Geschwisterchen 1002119, Geschwisterchen 1002121, Geschwisterchen 1002123, Geschwisterchen 1002124, Geschwisterchen 1002128, Geschwisterchen 1002129, Geschwisterchen 1002131, Geschwisterchen 1002133, Geschwisterchen 1002136, Geschwisterchen 1002137, Geschwisterchen 1002139, Geschwisterchen 1002140, Geschwisterchen 1002142, Geschwisterchen 1002149, Geschwisterchen 1002153, Geschwisterchen 1002155, Geschwisterchen 1002159, Geschwisterchen 1002161, Geschwisterchen 1002164, Geschwisterchen 1002170, Geschwisterchen 1002174, Geschwisterchen 1002175, Geschwisterchen 1002180, Geschwisterchen 1002183, Geschwisterchen 1002191, Geschwisterchen 1002193, Geschwisterchen 1002196, Geschwisterchen 1002198, Geschwisterchen 1002200, Geschwisterchen 1002203, Geschwisterchen 1002205, Geschwisterchen 1002208, Geschwisterchen 1002210, Geschwisterchen 1002211, Geschwisterchen 1002221, Geschwisterchen 1002230, Geschwisterchen 1002236, Geschwisterchen 1002241, Geschwisterchen 1002243, Geschwisterchen 1002245, Geschwisterchen 1002247, Geschwisterchen 1002252, Geschwisterchen 1002256, Geschwisterchen 1002258, Geschwisterchen 1002259, Geschwisterchen 1002269, Geschwisterchen 1002273, Geschwisterchen 1002275, Geschwisterchen 1002279, Geschwisterchen 1002280, Geschwisterchen 1002285, Geschwisterchen 1002286, Geschwisterchen 1002293, Geschwisterchen 1002295, Geschwisterchen 1002300, Geschwisterchen 1002301, Geschwisterchen 1002305, Geschwisterchen 1002309, Geschwisterchen 1002345, Geschwisterchen 1002349, Geschwisterchen 1002351, Geschwisterchen 1002371, Geschwisterchen 1002385, Geschwisterchen 1002391, Geschwisterchen 1002392, Geschwisterchen 1002397, Geschwisterchen 1002400, Geschwisterchen 1002406, Geschwisterchen 1002411, Geschwisterchen 1002414, Geschwisterchen 1002416, Geschwisterchen 1002420, Geschwisterchen 1002423, Geschwisterchen 1002425, Geschwisterchen 1002428, Geschwisterchen 1002433, Geschwisterchen 1002434, Geschwisterchen 1002445, Geschwisterchen 1002448, Geschwisterchen 1002450, Geschwisterchen 1002452, Geschwisterchen 1002454, Geschwisterchen 1002460, Geschwisterchen 1002464, Geschwisterchen 1002468, Geschwisterchen 1002470, Geschwisterchen 1002473, Geschwisterchen 1002474, Geschwisterchen 1002477, Geschwisterchen 1002481, Geschwisterchen 1002483, Geschwisterchen 1002486, Geschwisterchen 1002489, Geschwisterchen 1002492, Geschwisterchen 1002493, Geschwisterchen 1002498, Geschwisterchen 1002509, Geschwisterchen 1002511, Geschwisterchen 1002517, Geschwisterchen 1002519, Geschwisterchen 1002520, Geschwisterchen 1002523, Geschwisterchen 1002531, Geschwisterchen 1002534, Geschwisterchen 1002538, Geschwisterchen 1002552, Geschwisterchen 1002555, Geschwisterchen 1002558, Geschwisterchen 1002566, Geschwisterchen 1002567, Geschwisterchen 1002569, Geschwisterchen 1002570, Geschwisterchen 1002575, Geschwisterchen 1002577, Geschwisterchen 1002579, Geschwisterchen 1002581, Geschwisterchen 1002583, Geschwisterchen 1002587, Geschwisterchen 1002589, Geschwisterchen 1002591, Geschwisterchen 1002594, Geschwisterchen 1002597, Geschwisterchen 1002599, Geschwisterchen 1002604, Geschwisterchen 1002607, Geschwisterchen 1002613, Geschwisterchen 1002614, Geschwisterchen 1002622, Geschwisterchen 1002624, Geschwisterchen 1002627, Geschwisterchen 1002629, Geschwisterchen 1002632, Geschwisterchen 1002635, Geschwisterchen 1002638, Geschwisterchen 1002644, Geschwisterchen 1002648, Geschwisterchen 1002651, Geschwisterchen 1002657, Geschwisterchen 1002659, Geschwisterchen 1002662, Geschwisterchen 1002677, Geschwisterchen 1002678, Geschwisterchen 1002679, Geschwisterchen 1002684, Geschwisterchen 1002687, Geschwisterchen 1002688, Geschwisterchen 1002690, Geschwisterchen 1002698, Geschwisterchen 1002700, Geschwisterchen 1002703, Geschwisterchen 1002706, Geschwisterchen 1002711, Geschwisterchen 1002714, Geschwisterchen 1002730, Geschwisterchen 1002732, Geschwisterchen 1002735, Geschwisterchen 1002745, Geschwisterchen 1002746, Geschwisterchen 1002752, Geschwisterchen 1002755, Geschwisterchen 1002760, Geschwisterchen 1002768, Geschwisterchen 1002779, Geschwisterchen 1002780, Geschwisterchen 1002784, Geschwisterchen 1002786, Geschwisterchen 1002792, Geschwisterchen 1002793, Geschwisterchen 1002795, Geschwisterchen 1002796, Geschwisterchen 1002800, Geschwisterchen 1002808, Geschwisterchen 1002810, Geschwisterchen 1002814, Geschwisterchen 1002815, Geschwisterchen 1002817, Geschwisterchen 1002822, Geschwisterchen 1002823, Geschwisterchen 1002827, Geschwisterchen 1002832, Geschwisterchen 1002839, Geschwisterchen 1002840, Geschwisterchen 1002844, Geschwisterchen 1002850, Geschwisterchen 1002852, Geschwisterchen 1002855, Geschwisterchen 1002856, Geschwisterchen 1002861, Geschwisterchen 1002864, Geschwisterchen 1002865, Geschwisterchen 1002870, Geschwisterchen 1002874, Geschwisterchen 1002876, Geschwisterchen 1002877, Geschwisterchen 1002882, Geschwisterchen 1002885, Geschwisterchen 1002889, Geschwisterchen 1002891, Geschwisterchen 1002893, Geschwisterchen 1002896, Geschwisterchen 1002904, Geschwisterchen 1002906, Geschwisterchen 1002907, Geschwisterchen 1002912, Geschwisterchen 1002914, Geschwisterchen 1002918, Geschwisterchen 1002920, Geschwisterchen 1002921, Geschwisterchen 1002924, Geschwisterchen 1002925, Geschwisterchen 1002931, Geschwisterchen 1002937, Geschwisterchen 1002939, Geschwisterchen 1002941, Geschwisterchen 1002944, Geschwisterchen 1002947, Geschwisterchen 1002953, Geschwisterchen 1002957, Geschwisterchen 1002963, Geschwisterchen 1002966, Geschwisterchen 1002969, Geschwisterchen 1002970, Geschwisterchen 1002973, Geschwisterchen 1002977, Geschwisterchen 1002982, Geschwisterchen 1002984, Geschwisterchen 1002986, Geschwisterchen 1002990, Geschwisterchen 1002994,
ausblenden
Anwendungsgebiete von Polyedern
Aus der Perspektive der reinen Mathematik sind Polyeder vor allem schön und interessant und ihre Erforschung bedarf keiner weiteren Rechtfertigung. Dennoch kann man auch hier natürlich die Frage stellen, die fast genauso alt ist wie die Mathematik selber: Und wofür braucht man das eigentlich?
Ein wichtiges Anwendungsgebiet von Polyedern ist die Lineare Optimierung. Es handelt sich hierbei um eine Methode, die unter anderem in der Wirtschaft häufig verwendet wird, um Entscheidungen zu treffen, die von vielen Faktoren abhängen.
Im öffentlichen Nahverkehr ist das Planen der Netzlinien und Erstellen der Fahrpläne ein solches Problem. Viele Faktoren müssen berücksichtigt werden, wie Ankunfts-, Abfahrts- und Wegzeiten, Netzauslastung, Unterhaltskosten, Anzahl der zu befördernden Personen und so weiter. Die Verkehrsplaner müssen versuchen, den Verkehr flüssig zu gestalten und dabei die Kosten so gering wie möglich zu halten. Aus diesen Variablen entsteht ein System aus linearen Ungleichungen, deren Lösungsmenge ein Polytop bildet. Die optimalen Lösungen liegen in den Eckpunkten dieses Polytops. Um den effektivsten Fahrplan zu erstellen, müssen also die Eckpunkte des Polytops gefunden werden.
Wie kommen eigentlich die Namen von Mathematischen Objekten zustande?
Das Dreieck heißt „Dreieck“, weil es drei Ecken hat. Es hat aber auch drei Kanten. Unter einem Dreikant stellt man sich allerdings eher ein Werkzeug vor. Es reicht also nicht aus, dass der Name scheinbar schon eine Definition ist. Es ist zudem notwendig, dass der Name auch benutzt wird, damit sich seine Bedeutung einschleift.
Wie steht es aber mit mathematischen Objekten, die nach Mathematikerinnen und Mathematikern benannt wurden? An dieser Stelle kann man natürlich einwenden, dass wohl viel mehr Mathematiker Namenspatronen von Sätzen oder Konzepten sind als Mathematikerinnen. Um hervorzuheben, dass es sie aber doch gibt, sind an dieser Stelle sowohl die Noether-Ringe (nach Emmy Noether) als auch die Versiera der Agnesi (nach Maria Agnesi) zu nennen. Trotzdem besteht hier natürlich Aufholbedarf!
Wie kommt es zu diesen Namenskonventionen? Meistens werden Objekte, die mit einem Namen versehen werden, von anderen Wissenschaftlerinnen und Wissenschaftlern nach ihnen benannt. Das Konzept eines Ringes war ja zum Beispiel schon bekannt. Um dann die Ringe, über die Emmy Noether schrieb, von den allgemeinen unterscheiden zu können, sprach man eben über Noether-Ringe und so bürgerte sich zunächst eine Konvention und später eine Definition ein.
Dürers Vermutung hingegen hat nicht der Maler Albrecht Dürer selber geäußert. Auf ihn gehen allerdings die zugrundeliegenden Polyedernetze zurück. Die Frage selber stellte der Mathematiker G.C. Shephard im Jahr 1975, ohne sie allerdings so zu nennen. Warum dann im Folgenden von Dürers und nicht von Shephards Vermutung gesprochen wurde, darüber kann man nun spekulieren.
Zusammenfassend kann man also sagen, dass es keine Regeln oder Konventionen zur Namensvergabe gibt. Es verhält sich ähnlich wie mit der Vergabe von Spitznamen. Wenn alle wissen, wer oder was gemeint ist, dann bleibt der Name eben bestehen.