Glossary
Polyhedron
Polyhedra are geometrical bodies that consist of vertices, straight edges and flat faces. In our project we restrict ourselves to convex polyhedra. This means that all inner angles between two edges or two faces are less or equal to 180°. No cavities, holes or indentations are allowed.
The most prominent examples of polyhedra are the cube and the pyramid. You also may have encountered the prism or the octahedron. But there are so many more polyhedra.
The Platonic solids are a very symmetric and regular class of five polyhedra. They consist only of congruent (same shape and size), regular (all sides the same length) polygons. The tetrahedron, the octahedron and the icosahedron comprise of regular triangles. In every corner of the tetrahedron, three triangles meet. In the case of the octahedron four and with the icosahedron five triangles build a joint at each vertex. If you put six equilateral triangles at a vertex, which each have an interior angle of 60°, you get a full circle of 360° and they lie flat on the ground. Therefore, no new body emerges. Similarly, the cube is built from three squares and the dodecahedron from three equilateral pentagons at each vertex. Euclid used this approach in his proof to show that there can be no further polyhedra with these properties, thus classifying the five Platonic solids.


But symmetric polyhedra are not the only interest of mathematicians. For their research they are searching for polyhedra (or their higher-dimensional equivalent, the polytopes) that have specific properties. We have asked some geometers – this is what the mathematicians who study geometry are called – about their favorite polyhedra and this is what they said:
“If polytopes could be viewed as rocks, then the associahedron is the diamond of polytopes. Diamonds are made of a very common element in nature–carbon–and likewise the associahedron can be realized via very common tools. Yet it enjoys such a unique and rare structure–and provides such a fascination–that no other polytope may ever be compared to the diamond.” - Jean-Philippe Labbé.
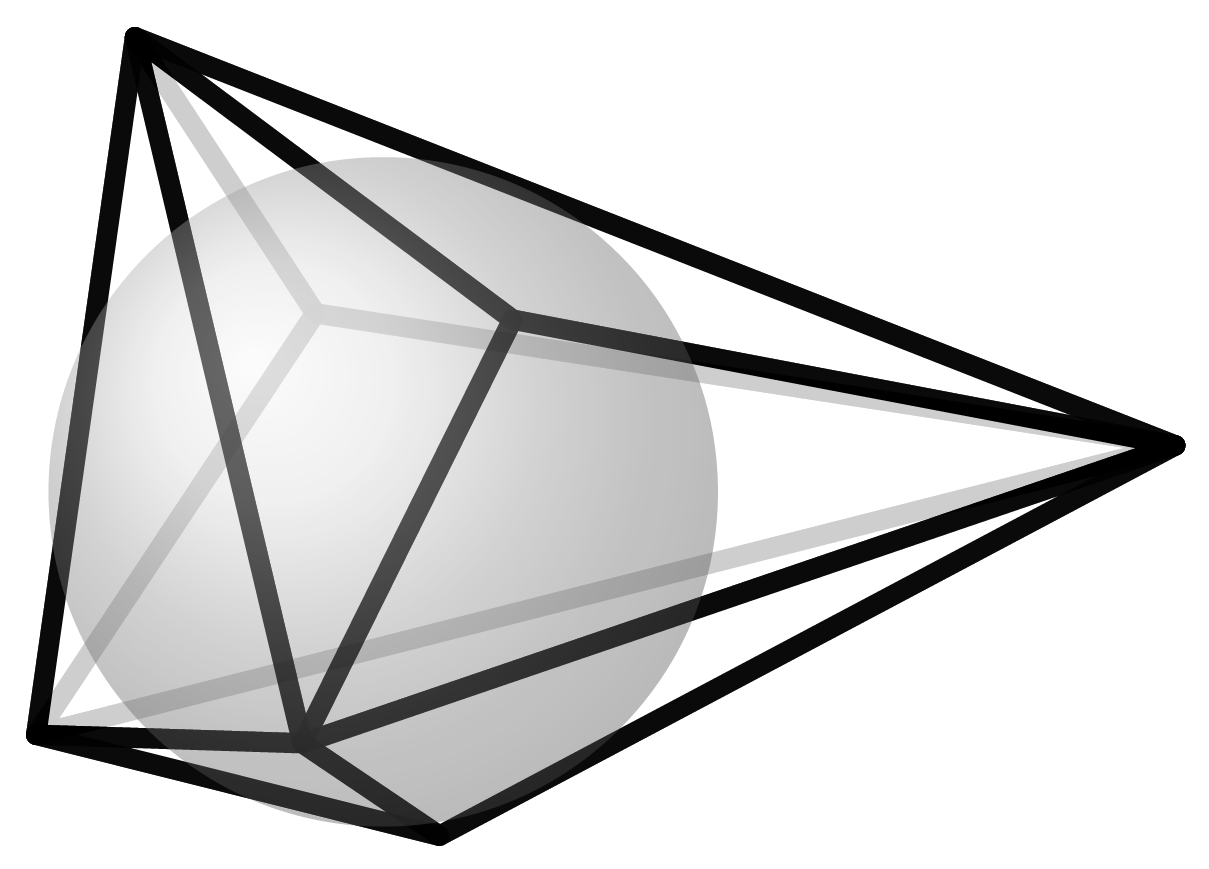
“My favorite 3-polytope is the icosahedron, for its complexity yet simplicity. If you start gluing equilateral triangles, five at a vertex, and no matter what you do you end up with this nice thing. When I got bored in high school (which, yes, happened), I drew icosahedra in the margins in my notebooks. Sometimes they were not totally regular; I amused myself making them look like faces. Last but not least, I am fascinated by the fact that you can decompose its 12 vertices into three golden rectangles intertwined as Borromean rings.” - Francisco Santos.

“My favourite polyhedron is “Miller’s solid”, also known as the ”pseudo-rhombicuboctahedron“ or as the ”elongated square gyrobicupola“, probably first found by D. M. Y. Sommerville in 1905 — an object that was often overlooked (already by Archimedes?), discovered and rediscovered (by J. C. P. Miller, among others). It is pretty, but if you look closely it has a certain twist, so it is not perfect. It looks classical, like an Archimedean solid, but it isn’t really, at least according to the modern definition of an Archimedean solid. Thus it is a good reminder that we have to be careful with definitions in mathematics, and always look at possible exceptions and special cases.” - Günter M. Ziegler.
„My favourite polyhedra are the Koebe polyhedra. All their edges touch a sphere. All faces of these polyhedra have inscribed discs. The discs of neighbouring faces touch. These exist an explicit dualization procedure that generates discrete minimal surfaces from Koebe polyhedra. The corresponding surface is then a discrete P-Schwarz surface and the Koebe polyhedron is its Gauss map. One can read more in: A.I. Bobenko, T. Hoffmann, B.A. Springborn, Minimal surfaces from circle patterns: Geometry from combinatorics, Ann. of Math. 164:1 (2006) 231-264) and can watch the movie: (http://discretization.de/en/movies/koebe/).“ - Alexander Bobenko.
Polygon
A polygon is a two-dimensional polyhedron which consists of vertices and edges. The area bounded by the edges is the polygon itself. Three-dimensional polyhedra are made up of vertices, edges and polygons, i.e., the faces.
A special class of polygons are called the regular polygons. They are made up of equilateral edges (all the same length) and all their inner angles are the same. Some examples of regular polygons are the square, equilateral triangle, and equilateral pentagon. Regular polygons form the building blocks for the Platonic and Archimedean solids.
Polyhedral Nets
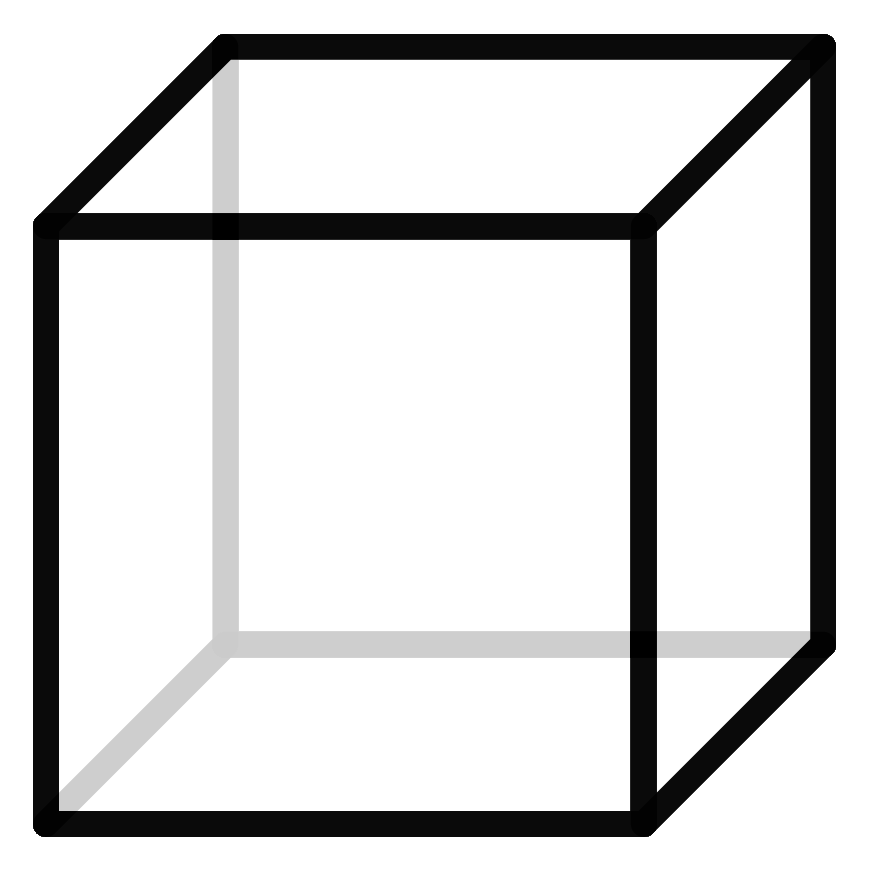
If you cut a hollow cube on enough edges, unfold it and lay it flat on the plane, you get what is called the net of the cube. If you draw this net on paper, you get an outline which you can cut out and glue together to form the cube. Of course, this method works for any polyhedra. In our project, we use exactly these templates to build our models. We simulated this process of cutting open and unfolding polyhedra with a computer and automatically created the nets of the polyhedra.
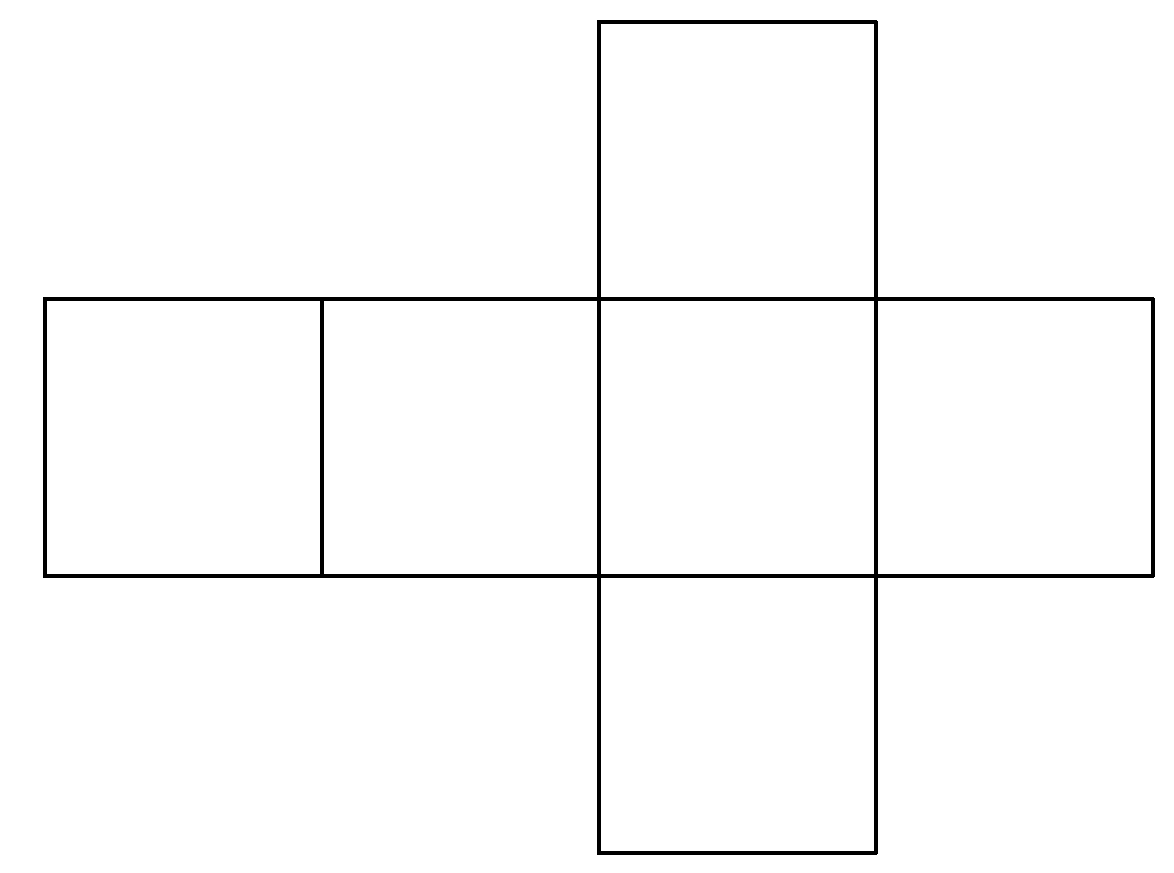
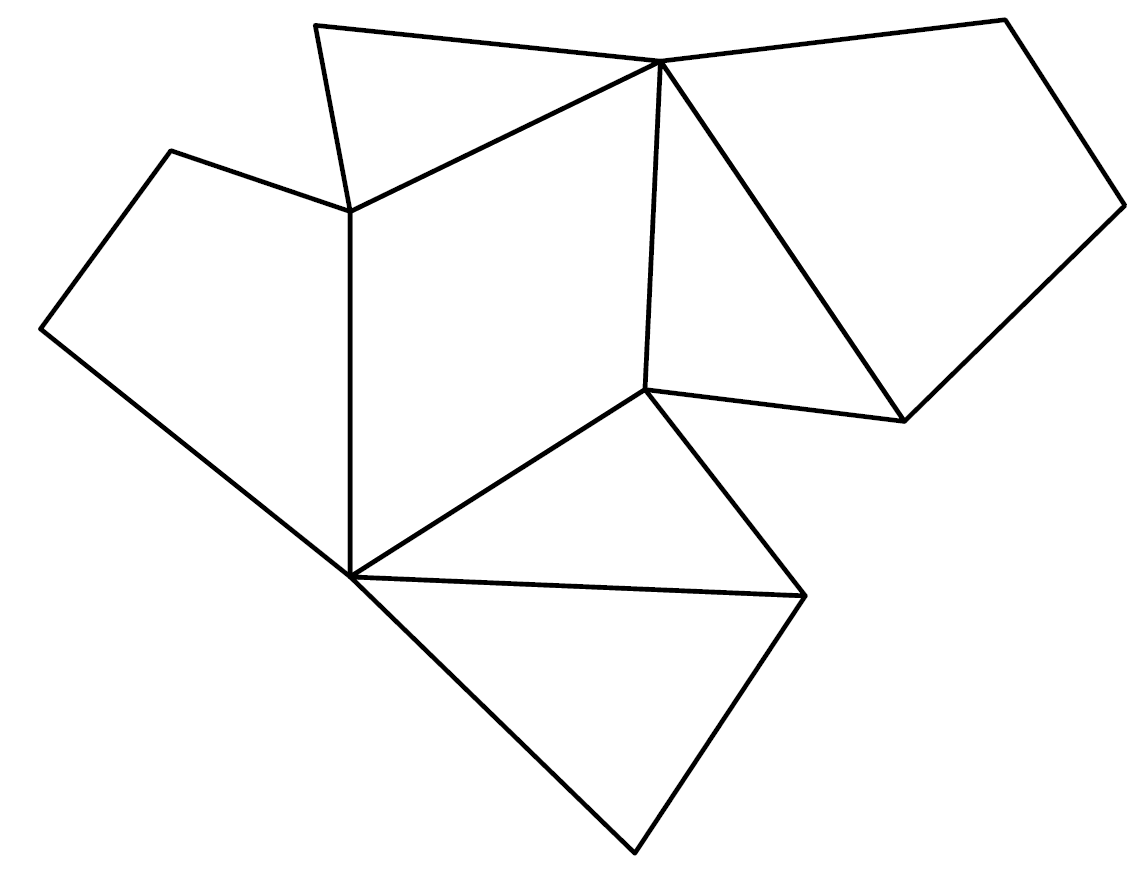
A cube with its net and a polygon with seven corners and the associated net.
Archimedian Solids
Another very symmetric and hence “beautiful” class of polyhedra are the Archimedean Solids. They also only consist of regular polygons, but here unlike the Platonic Solids a combination of them is allowed. The most common representative is the soccer ball. Mathematicians would rather speak of a truncated icosahedron, since it emerges when you chop off the tip of each vertex of an icosahedron.

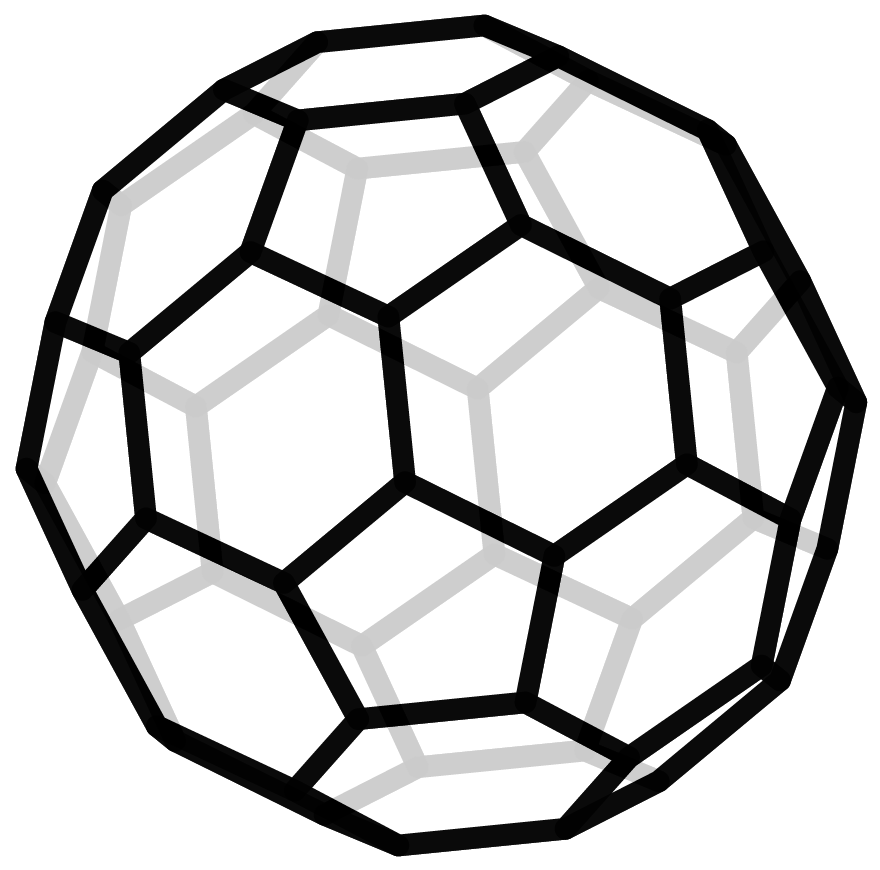
On the left an icosahedron and on the right its truncation - a soccer ball.
How many polyhedra are there?
For every fixed number of vertices, there are a certain number of polyhedra. In the table, the number of different types of polyhedra is given for the number of vertices. It is clear that the number of types increases rapidly. If you have four points in space, they are either all on the same level (not three-dimensional), or the shape will be a pyramid over a triangle. Therefore, there is only one polyhedron with four vertices, the tetrahedron.
| Ecken | Polyeder |
| 4 | 1 |
| 5 | 2 |
| 6 | 7 |
| 7 | 34 |
| 8 | 257 |
| 9 | 2.606 |
| 10 | 32.300 |
| 11 | 440.564 |
| 12 | 6.384.634 |
| 13 | 96.262.938 |
| 14 | 1.496.225.352 |
| 15 | 23.833.988.129 |
| 16 | 387.591.510.244 |
| 17 | 6.415.851.530.241 |
| 18 | 107.854.282.197.058 |
| 19 | ??? |
For five vertices, there are two possibilities: the pyramid over the square, if four of the five vertices lie the same plane, or the double pyramid over a triangle. For six vertices, finding the seven different types starts to get more complicated.
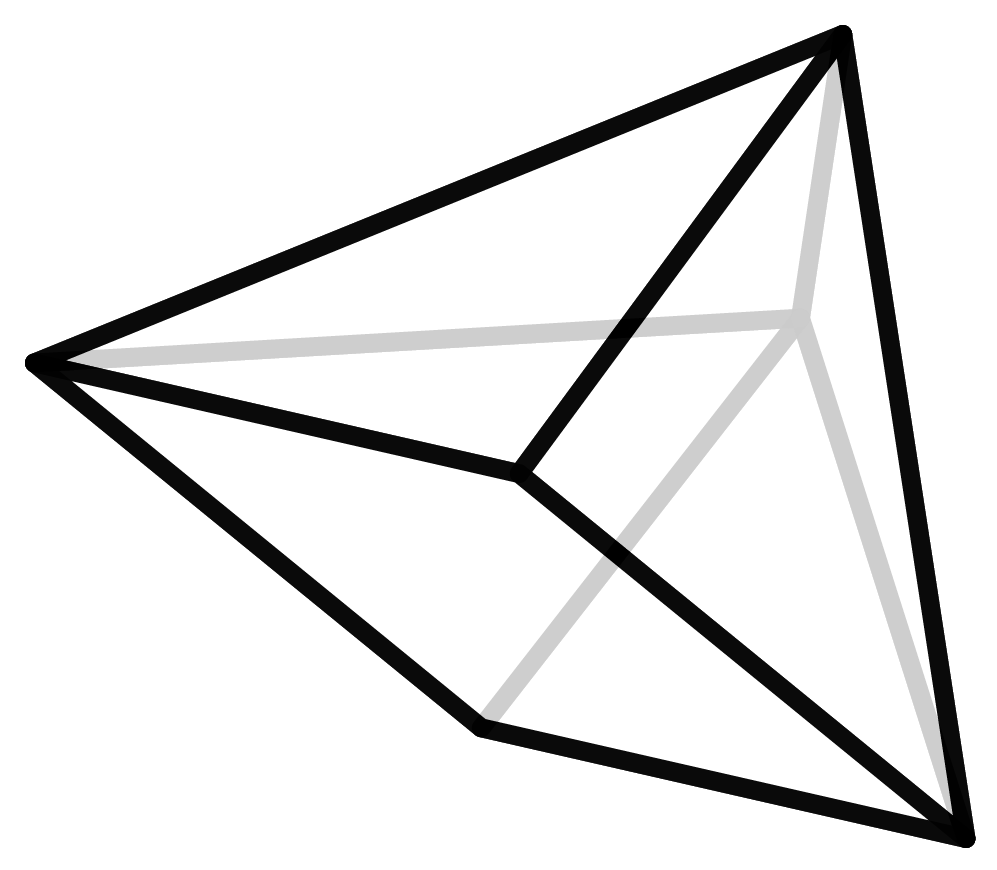

In order to find out how many polyhedra types actually exist for each number of vertices, we have to create and list them. But how do you know that this list is complete and no polyhedron is counted twice? In geometry, Steinitz’s Theorem states that each polyhedron can be uniquely assigned to a graph with certain properties. (Here the notion of a graph is not referring to the ones living in coordinate systems but the ones that are subject to graph theory). These graphs are mathematically easier to grasp and therefore count. But even for this, you will need a computer because the numbers get very large very fast. The number of seven- and eight-vertice polyhedra, 34 and 257 respectively, were found back in 1899. For the discovery of the 2606 nine-vertice polyhedra in the year 1969 the invention of the computer was necessary.
Dimension
In mathematics, there are many ways to interpret dimensions. One way is to imagine dimensions as the number of variables. For example, the ingredients of an apple pie (flour, butter, sugar, eggs, baking soda and apples) can be understood as six variables and therefore the apple pie is a six-dimensional object.
By looking at photos and films, which are a representation of our three-dimensional world in a two-dimensional medium, we are used to seeing an extra dimension. This process of mapping a higher dimension into a lower one, that is taking a two-dimensional photograph of the three-dimensional world, is called a projection in mathematics.
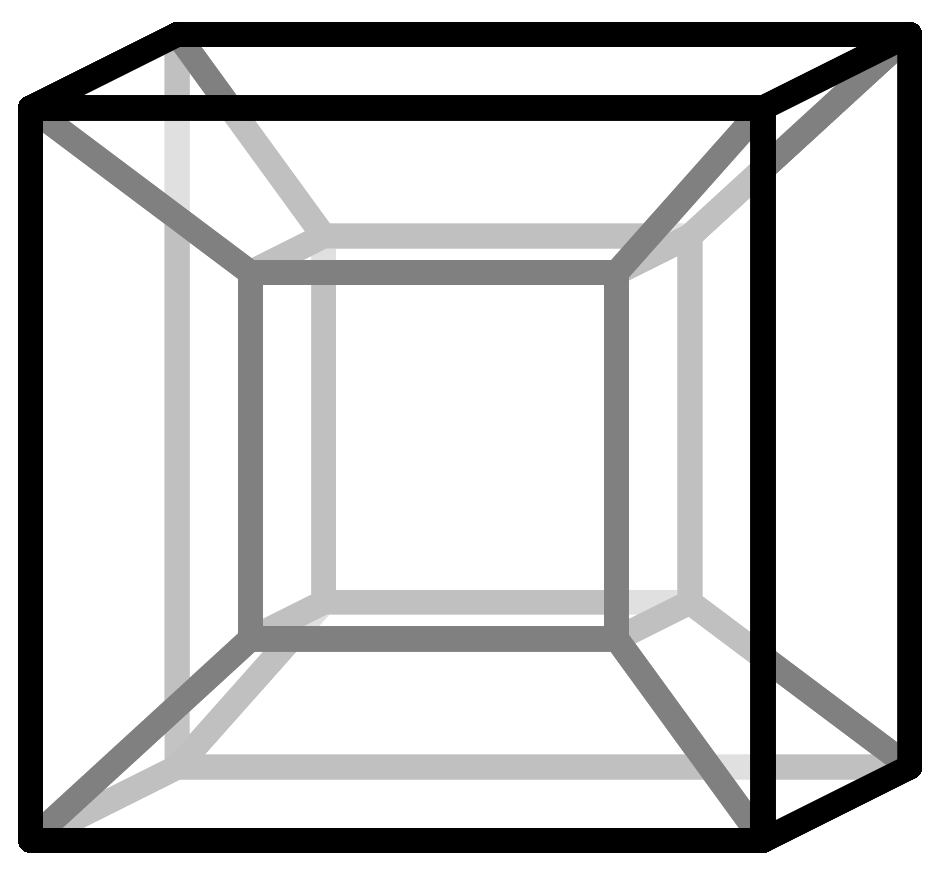
Unfortunately, it is not possible to truly represent four-dimensional space in the three-dimensional space surrounding us, but we can use projections to understand it. For example, if you look at a cube, its faces are squares. A square can be thought of as a two-dimensional cube, because all its sides are the same length, so the sides of the three-dimensional cube are two-dimensional cubes. This idea extends to higher dimensions. The side surfaces of a four-dimensional cube are three-dimensional cubes. The result is a so-called tesseract. Here is a link to a video where this relationship is graphically visualized.
Convex/Convexity
When we speak of polyhedra, we silently assume that they are convex polyhedra. Convex means that there are no indentations, cavities or holes. The mathematical definition of convexity states that for any two points that lie within a set, a straight line connecting them must lie completely within the set.
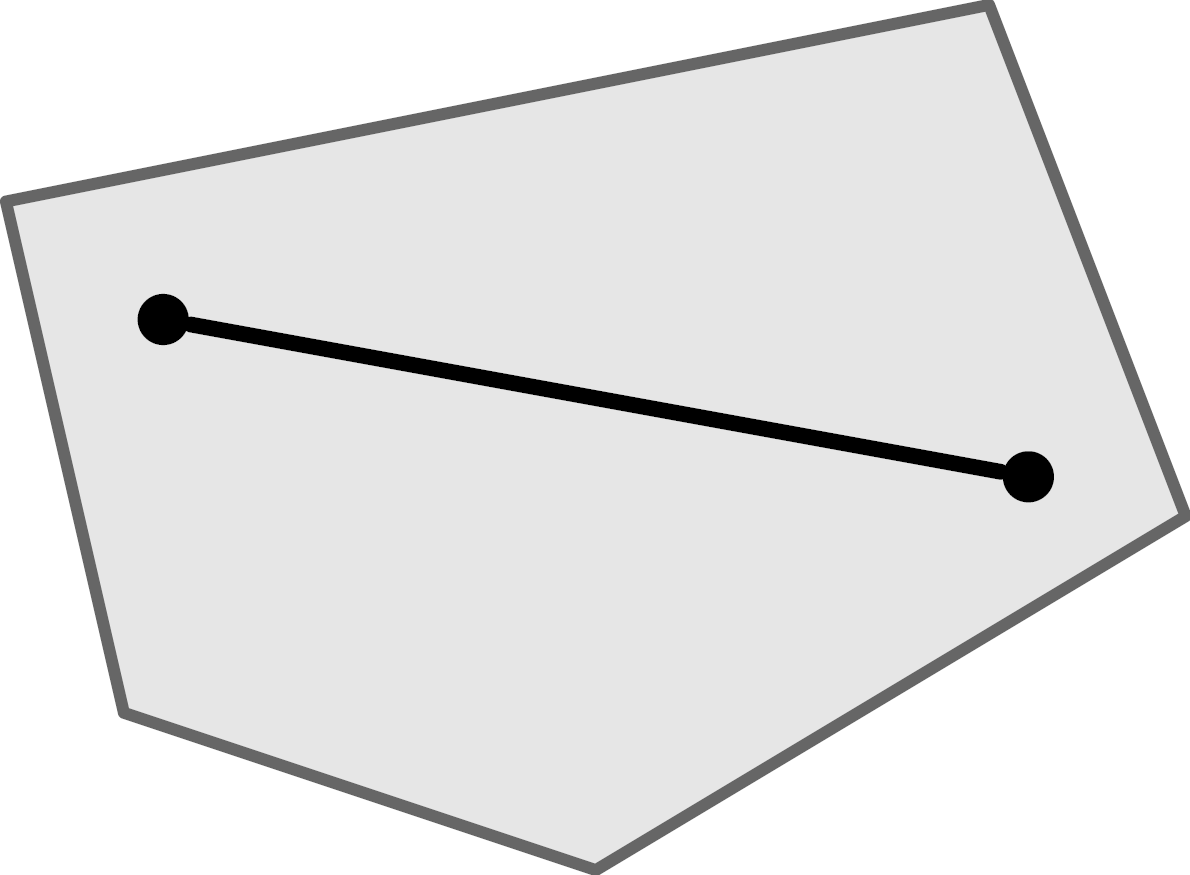
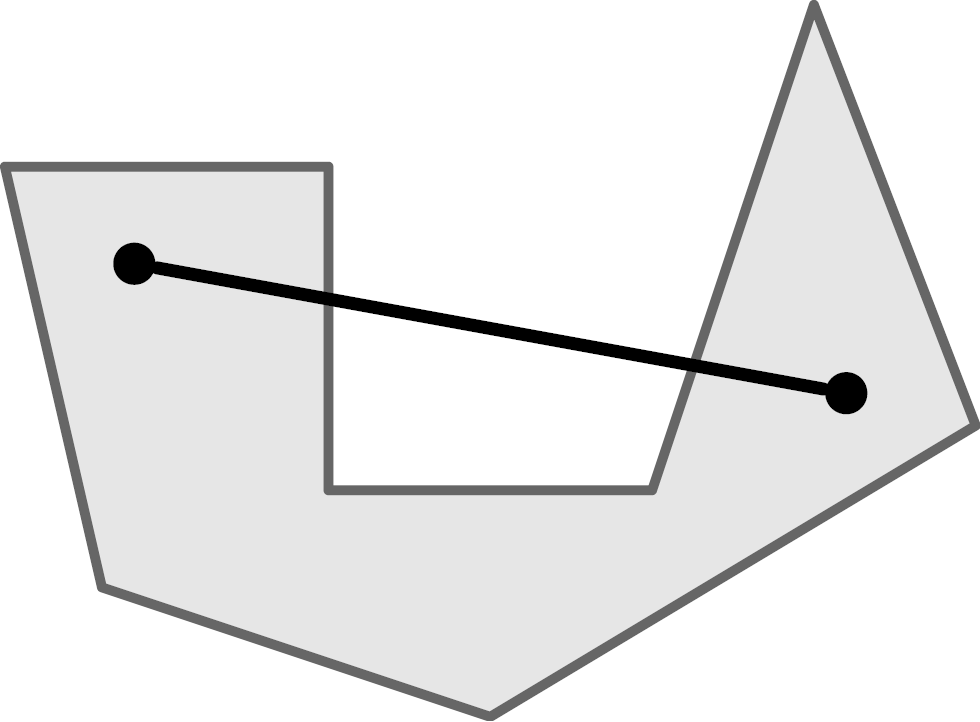
On the left a convex, on the right a non-convex object.
Combinatorial Type
Each polyhedron can be geometrically realized in different ways. It can be big or small, and its shape can also be changed, as long as the structure of the vertices, edges and surfaces remains the same. This structure, which is the number of edges meeting at the vertices, and the number of vertices belonging to each surface, is called the combinatorial type of a polyhedron. We call two polyhedra combinatorially equivalent if they possess the same combinatorial type, i.e., one can uniquely assign vertices to each other so that if two vertices in one polyhedron are connected by an edge, then the vertices in the other polyhedron are connected by an edge. Every polyhedron has an infinite number of different geometric interpretations. If you choose a polyhedron on Polytopia.eu, you will adopt the entire combinatorial type. So you have actually adopted infinitely many polyhedra. To make it less confusing and easier to make the model, we have chosen a clear realization of the polyhedron. These are the so-called Koebe-Andreev-Thurston realizations of polyhedra. In particular, these realizations have a sphere inscribed inside the polyhedra that touches each of the edges at exactly one point. In particular, each surface contains a circle that touches the edges just once.

f-Vector
The f-vector of the polyhedron indicates how many vertices, edges, and faces it has. A vector in this case is not a geometric quantity but only the way of representing these numbers. The cube consists of 8 vertices, 12 edges, and 6 faces, and thus has the f-vector (8,12,6). However, the polyhedra are not uniquely determined by this vector. There may be other polyhedra with the same f-vector that have a completely different structure. We call these polyhedra siblings.

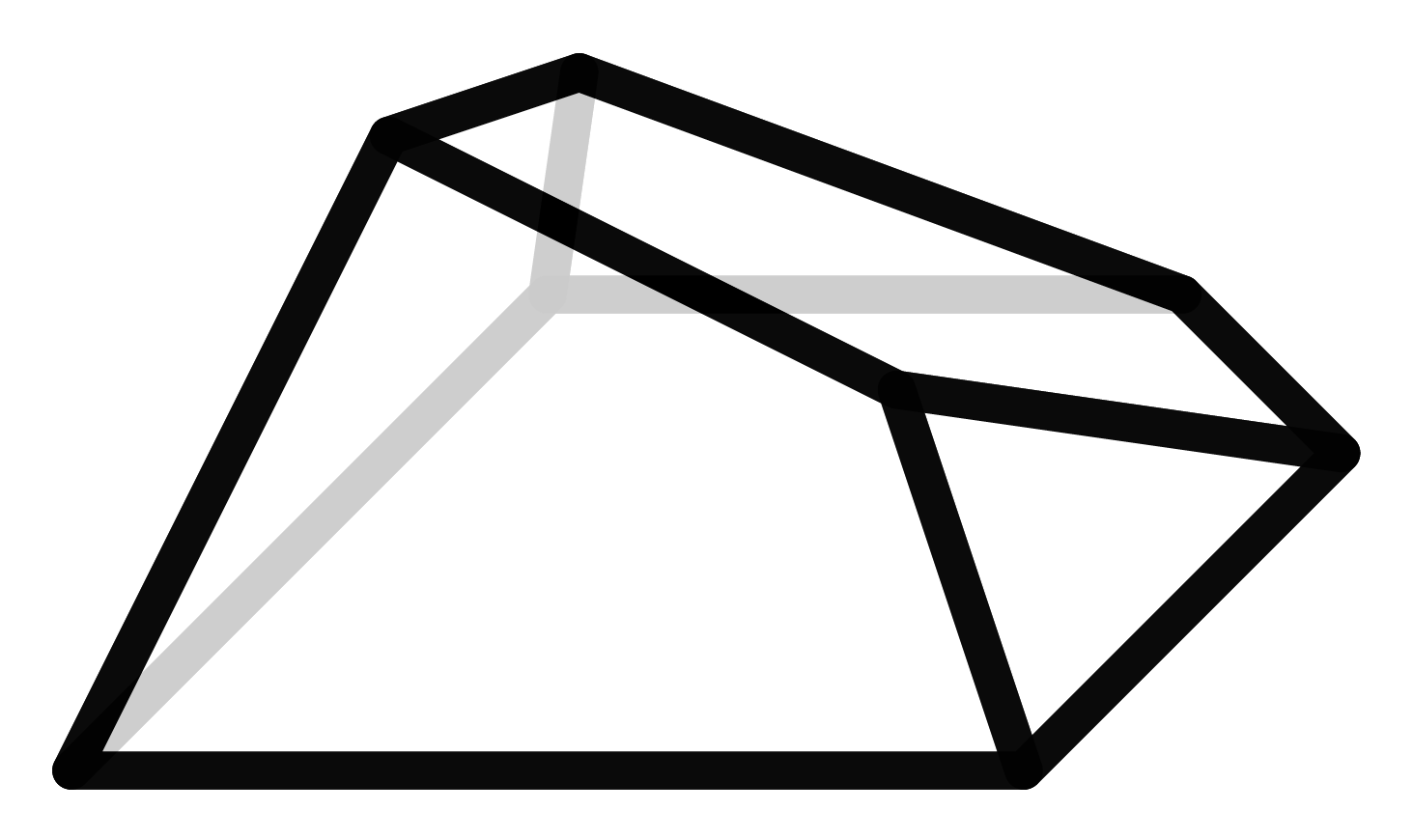
Here we see a cube and its sister. She also possesses 6 faces, 12 edges, and 8 vertices but contains an entirely different structure that the cube.
Mathematical Models
Physical models and their construction have long played an important role in mathematics. For one thing, there was simply no other way to understand ideas in a three-dimensional environment. Of course, three-dimensional models can always be drawn, but then the drawing is only a projection of the model onto the plane, much like taking a picture of the model. When it comes to photos of familiar objects, recognizing the space does not cause us any problems, because we know, for example, that a table is usually right-angled. If we see a perspectively distorted table in a photo, we intuitively know about the right angles. Of course, this intuition is not there when trying to understand the structure of an unfamiliar geometric object. In order to recognize certain properties, such as an axis of symmetry, it is very helpful to actually hold an object in your hand and turn it.
Models serve not only to gain knowledge but also to share knowledge. To make their research accessible to others, mathematicians needed a way to visualize it. Nowadays, this is done mainly with computers. There is a lot of software to generate mathematical and geometric graphics. Rotation of a model using this software also counteracts the problem of restriction to the flat screen.
Dürer’s Conjecture
Although mathematicians have been dealing with polyhedra since ancient times, not everything is known about them. For one thing, every question that is answered only brings about new questions. For example, the number of three-dimensional polyhedra is known only up to 18 vertices. If somebody should find out how many polyhedra there are with 19 vertices, one can immediately ask about the number of polyhedra with 20 vertices. There are also questions that have been waiting a long time for an answer. A „nice“ example, because it is easy to understand and yet still an unsolved problem, is the so-called Dürer conjecture. The painter Albrecht Dürer spent some years studying mathematics and the concept of the net of a polyhedron goes back to him. In his book, „The Painter’s Manual“ he drew nets of several polyhedra.
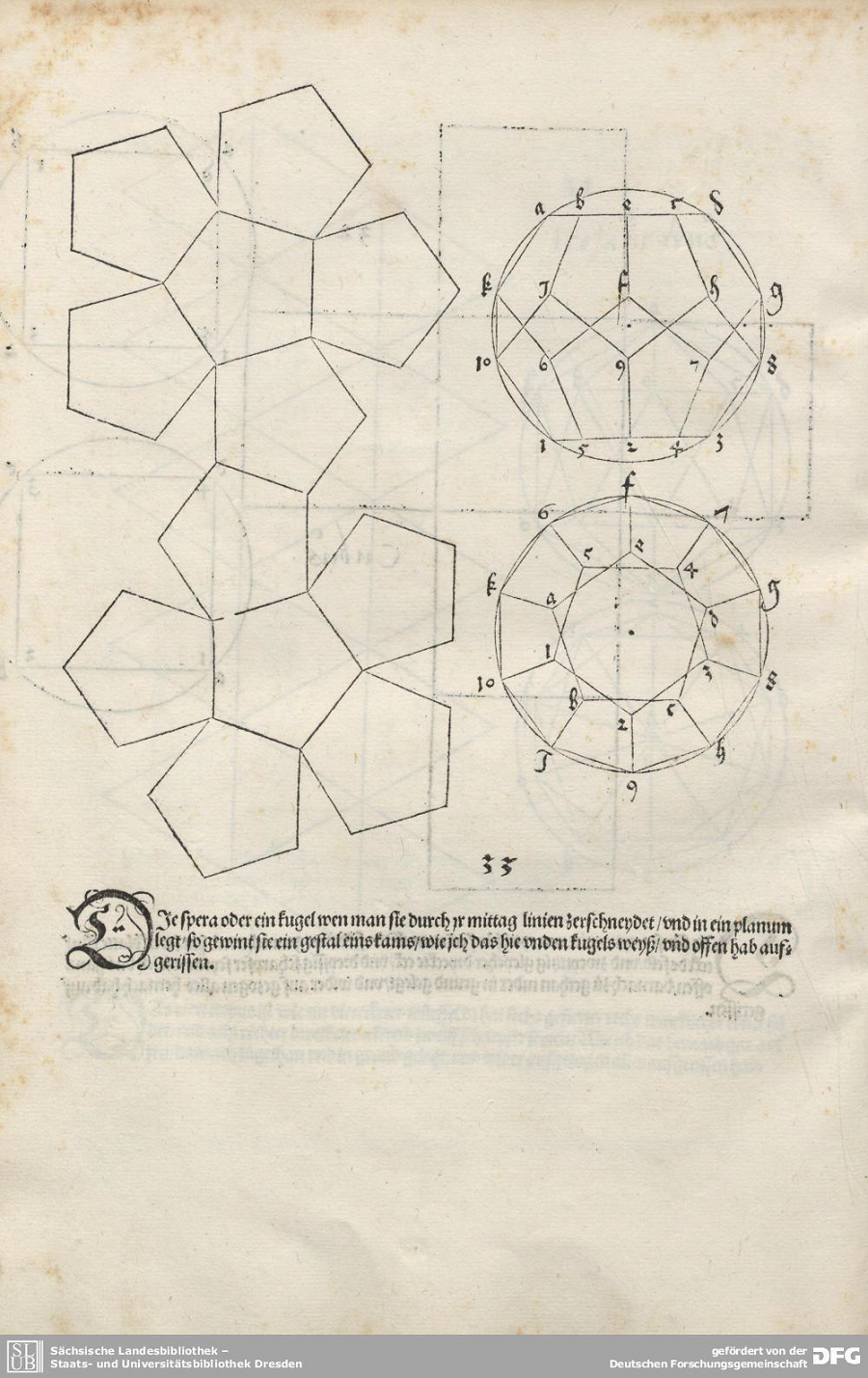
A net of a polyhedron is created by considering the polyhedron as an empty shell, which is cut along its edges in such a way that it remains connected but can be laid flat without distorting the faces. The question behind Dürer’s conjecture is whether this is possible for every polyhedron such that the faces do not overlap when it is unfolded. In other words, does every polyhedron have a net?
To date, many mathematicians have considered this question and there are some intermediate results. For example, it is known that you can unfold any polyhedron without overlap if you pull and distort the faces and thus change its geometrical realization but not its structure (s. https://arxiv.org/pdf/1305.3231.pdf). The only polyhedron for which we know for sure that can always be unfolded without changing its geometrical structure is the tetrahedron.
Since we have automatically generated the unfoldings for the polyhedra in our project, it is possible that the net of your adopted polyhedron is overlapping. If so, write us an email!
Siblings
Polyhedra are siblings if they contain the same number of vertices, edges and faces, hence the same f-vector. Similar to human siblings, some polyhedral siblings do look alike each other while others have a completely different form. The cube consists of 8 vertices, 12 edges and 6 faces. These numbers do not uniquely define its structure. There are polyhedra who have the same f-vector but an entirely different structure.
Siblings:Eckaihedron, Harri Edder , Tayloreder , Andreas, Sibling 1000006, Sibling 1000036, Sibling 1000063, Sibling 1000067, Sibling 1000068, Sibling 1000073, Sibling 1000079, Sibling 1000081, Sibling 1000095, Sibling 1000098, Sibling 1000101, Sibling 1000103, Sibling 1000108, Sibling 1000109, Sibling 1000111, Sibling 1000113, . . .
Sibling 1000212, Sibling 1000213, Sibling 1000241, Sibling 1000243, Sibling 1000257, Sibling 1000258, Sibling 1000273, Sibling 1000277, Sibling 1000282, Sibling 1000286, Sibling 1000289, Sibling 1000291, Sibling 1000293, Sibling 1000294, Sibling 1000297, Sibling 1000326, Sibling 1000337, Sibling 1000359, Sibling 1000366, Sibling 1000368, Sibling 1000369, Sibling 1000370, Sibling 1000374, Sibling 1000376, Sibling 1000379, Sibling 1000381, Sibling 1000385, Sibling 1000391, Sibling 1000392, Sibling 1000395, Sibling 1000397, Sibling 1000401, Sibling 1000415, Sibling 1000435, Sibling 1000437, Sibling 1000439, Sibling 1000444, Sibling 1000470, Sibling 1000502, Sibling 1000505, Sibling 1000511, Sibling 1000579, Sibling 1000599, Sibling 1000627, Sibling 1000630, Sibling 1000631, Sibling 1000633, Sibling 1000637, Sibling 1000646, Sibling 1000647, Sibling 1000663, Sibling 1000666, Sibling 1000673, Sibling 1000679, Sibling 1000681, Sibling 1000682, Sibling 1000686, Sibling 1000689, Sibling 1000691, Sibling 1000700, Sibling 1000702, Sibling 1000703, Sibling 1000743, Sibling 1000746, Sibling 1000752, Sibling 1000753, Sibling 1000758, Sibling 1000763, Sibling 1000786, Sibling 1000787, Sibling 1000790, Sibling 1000795, Sibling 1000796, Sibling 1000798, Sibling 1000802, Sibling 1000806, Sibling 1000812, Sibling 1000815, Sibling 1000816, Sibling 1000881, Sibling 1000911, Sibling 1000913, Sibling 1000932, Sibling 1000936, Sibling 1000937, Sibling 1000957, Sibling 1000966, Sibling 1000969, Sibling 1000970, Sibling 1000971, Sibling 1000980, Sibling 1000982, Sibling 1000984, Sibling 1000987, Sibling 1000994, Sibling 1000996, Sibling 1000997, Sibling 1001000, Sibling 1001026, Sibling 1001028, Sibling 1001030, Sibling 1001033, Sibling 1001044, Sibling 1001076, Sibling 1001078, Sibling 1001081, Sibling 1001083, Sibling 1001085, Sibling 1001096, Sibling 1001098, Sibling 1001100, Sibling 1001105, Sibling 1001134, Sibling 1001179, Sibling 1001183, Sibling 1001185, Sibling 1001197, Sibling 1001225, Sibling 1001234, Sibling 1001237, Sibling 1001244, Sibling 1001245, Sibling 1001259, Sibling 1001263, Sibling 1001268, Sibling 1001271, Sibling 1001274, Sibling 1001276, Sibling 1001281, Sibling 1001282, Sibling 1001284, Sibling 1001287, Sibling 1001289, Sibling 1001297, Sibling 1001305, Sibling 1001307, Sibling 1001309, Sibling 1001313, Sibling 1001318, Sibling 1001319, Sibling 1001322, Sibling 1001330, Sibling 1001372, Sibling 1001416, Sibling 1001419, Sibling 1001421, Sibling 1001425, Sibling 1001435, Sibling 1001466, Sibling 1001516, Sibling 1001520, Sibling 1001522, Sibling 1001524, Sibling 1001537, Sibling 1001539, Sibling 1001540, Sibling 1001548, Sibling 1001550, Sibling 1001553, Sibling 1001598, Sibling 1001613, Sibling 1001615, Sibling 1001617, Sibling 1001621, Sibling 1001628, Sibling 1001632, Sibling 1001633, Sibling 1001635, Sibling 1001641, Sibling 1001642, Sibling 1001664, Sibling 1001666, Sibling 1001672, Sibling 1001673, Sibling 1001678, Sibling 1001685, Sibling 1001688, Sibling 1001690, Sibling 1001697, Sibling 1001700, Sibling 1001704, Sibling 1001707, Sibling 1001710, Sibling 1001711, Sibling 1001717, Sibling 1001797, Sibling 1001825, Sibling 1001865, Sibling 1001888, Sibling 1001929, Sibling 1001932, Sibling 1001934, Sibling 1001940, Sibling 1001944, Sibling 1001947, Sibling 1001948, Sibling 1001953, Sibling 1001956, Sibling 1001959, Sibling 1001960, Sibling 1001964, Sibling 1001968, Sibling 1001971, Sibling 1001976, Sibling 1002003, Sibling 1002006, Sibling 1002009, Sibling 1002010, Sibling 1002015, Sibling 1002023, Sibling 1002025, Sibling 1002027, Sibling 1002030, Sibling 1002036, Sibling 1002041, Sibling 1002044, Sibling 1002045, Sibling 1002050, Sibling 1002052, Sibling 1002058, Sibling 1002060, Sibling 1002064, Sibling 1002086, Sibling 1002091, Sibling 1002105, Sibling 1002150, Sibling 1002214, Sibling 1002217, Sibling 1002222, Sibling 1002227, Sibling 1002238, Sibling 1002264, Sibling 1002311, Sibling 1002314, Sibling 1002318, Sibling 1002321, Sibling 1002326, Sibling 1002328, Sibling 1002329, Sibling 1002332, Sibling 1002333, Sibling 1002336, Sibling 1002342, Sibling 1002357, Sibling 1002360, Sibling 1002363, Sibling 1002365, Sibling 1002367, Sibling 1002373, Sibling 1002375, Sibling 1002378, Sibling 1002382, Sibling 1002402, Sibling 1002407, Sibling 1002417, Sibling 1002437, Sibling 1002441, Sibling 1002502, Sibling 1002514, Sibling 1002539, Sibling 1002542, Sibling 1002548, Sibling 1002561, Sibling 1002562, Sibling 1002563, Sibling 1002641, Sibling 1002654, Sibling 1002668, Sibling 1002670, Sibling 1002674, Sibling 1002708, Sibling 1002723, Sibling 1002726, Sibling 1002738, Sibling 1002740, Sibling 1002742, Sibling 1002762, Sibling 1002772, Sibling 1002775, Sibling 1002829, Sibling 1002915,
hide
Fields of Application of Polyhedra
From a purely mathematical perspective, polyhedra are, above all, beautiful and interesting, and their exploration requires no further justification. Nevertheless, one can obviously ask the question, which is almost as old as mathematics itself, what do you really need it for?
One important application of polyhedra is Linear Optimization. It is a method that is often used in business, among other areas, to make decisions that depend on many factors.
One example is making a timetable and network line for a public transportation system. There are many variables to be considered, such as arrival and departure times, operational costs, line capacities and so on. City planners want to meet public expectations for how often a train comes and also minimize the costs, run enough trains to carry enough passengers, but are also limited to the number of trains on the tracks for safety reasons. From these variables, a system of linear inequalities arise and their set of possible solutions form a polytope. The optimal solutions are located at the vertices of that polytope. So finding these vertices gives city planners optimal ways to build the most effective timetable possible.
How do the names of mathematical objects actually come about?
The Greek word for five is “penta”, so a pentagon is a five sided polygon. The hexagon, heptagon, and octagon get their names in the same way, but there is no trigon. Instead, a triangle is the 3-sided polygon and gets its name from its three angles. But then what is a square? Clearly, it is not enough that the name alone can give a definition. Although “square” does not describe the features, it is a commonly known shape. Therefore, it is necessary to actually use the name so that its meaning is well known.
Mathematical objects are also often named after mathematicians. More often than not, these objects and other concepts have been named after male mathematicians, but female mathematicians have also left a legacy behind. The Noetherian rings, named after Emmy Noether, and the Witch of Agnesi, after Maria Agnesi are some examples, but there is a need to close the gender gap.
Mostly, the objects that are named after mathematicians are given these names by scientists. The concept of a ring was already known, but to be able to distinguish the rings that Emmy Noether wrote about from the general ones, one talked about Noetherian rings. The convention of these rings came first and later a definition was established.
The Dürer conjecture was never proposed by the painter Albrecht Dürer himself but the underlying nets of polyhedra go back to him. The conjecture itself was posed by the mathematician G. C. Shephard in 1975. Why then it is known as Dürer’s and not Shephard’s conjecture, one can only speculate.
In summary, the rules and conventions for naming are rather ambiguous. It is similar to getting a nickname – if everyone knows who or what is meant, then the name sticks.